Kütle Transferi;Kristalizasyon (crystallization)

Kristalizayon, homojen bir faz içinde katı partiküllerin oluşmasıdır. Örneğin, bir buhar içinde (kar gibi) katı taneciklerin oluşması, büyük tek kristallerin üretiminde sıvı bir ergiyikten katılaşma veya sıvı çözeltiden kristalizasyon tipik örneklerdir. Bu bölümde özellikle sıvı çözeltiden kristalizasyon üzerinde durulacaktır.

Çözeltiden kristalizasyon, kristal formda malzemelerin çeşitliliğine olanak verdiğinden endüstriyel yönden oldukça önemlidir. Bunun nedeni iki temele dayanır: Birincisi saf olmayan bir çözeltiden oluşan bir kristal, kristal karışımları karışımları halinde bulunmadıkça, saftır. Diğeri, uygun koşullar için, paketlenip depolandığında saf kimyasal maddelerin elde edilmesinde pratik bir yöntemdir.

Magma: Endüstriyel olarak çözeltiden kristalizasyonda, ana sıvı ve çeşitli boyutlardaki kristallerin iki-fazlı karışımına ‘magma’ denir; magma, kristalizörden ürün olarak çekilir.

Kristal Boyutunun Önemi: Kristalizasyonda temizlik, iyi verim ve yüksek saflık öncelikli hedeflerdir; ancak, bir kristal ürünün görünümü ve boyut dizisi de önemlidir. Kristaller daha sonra işlemden geçirilecekse, süzme, yıkama, bazı kimyasal maddelerle etkileşim, taşıma ve depolama gibi, makul seviyelerde boyut ve boyut kararlılığına gereksinim vardır. Kristal ‘son ürün’ olarak işaretlendiyse, alıcı, kuvvetli, birbirine yapışmamış, standart boyutlarda ve kabuklaşmamış bireysel (tek) kristaller ister.

1. KRİSTAL GEOMETRİSİ

Bir kristal, cansız maddeler arasında en yüksek organize tipe sahip bir maddedir. Kristal, uzam (mekan) latisleri denilen düzenli üç-boyutlu dizilerde düzenlenmiş oluşturucu (kurucu) partikülleriyle, -ki bunlar atomlar, moleküller veya iyonlardır-karakterize edilir. Partiküllerin böyle düzenlenmelerinin bir sonucu olarak, kristaller oluşmaya bırakıldığında (dış etkenler ve diğer kristallerin etkilerinin olmadığı koşullarda) polihedron formunu alır; keskin köşelere ve düz kenarlara veya yüzeylere sahiptir. Aynı malzemenin çeşitli kristallerinin tüm kenar ve yüzey boyutları relatif olarak farklı olmasına rağmen, uygun yüzeylerin oluşturduğu açılar eşittir ve aynı malzemeyi karakterize eder.

Kristalografik Sistemler: Belirli bir substansın (madde, cisim, ..) tüm kristalleri, bireysel yüzeylerinin farklılığına rağmen, aynı arayüzey açısına sahiptir; kristal formları bu açılar temel alınarak sınıflandırılır. Yedi kristal formu: kübik, heksagonal, trigonal, tetragonal, ortorombik, monoklinik ve trikliniktir. Bir malzeme, kristalizasyon koşullarına bağlı olarak iki veya daha fazla farklı sınıfta kristallenebilir. Örneğin, kalsyum karbonat doğal olarak genellikle heksagonal formda (kalsit) bulunurken, ortorombik formu (aragonit)) da vardır.

Değişmeyen Kristaller: İdeal koşullar altında, büyüyen bir kristal geometrik benzerliğini korur; böyle bir kristale ‘değişmeyen (invaryant)’ denir. Şekil-1’de, değişmeyen bir kristalin büyüme esnasındaki enine kesiti görülmektedir; her bir poligon farklı zamanlardaki kristal taslağını tanımlar. Kristal değişmeyen olduğundan bu poligonlar geometrik olarak benzerdir ve poligonların köşelerini kristalin merkeziyle birleştiren noktalı çizgiler düzdür. Merkez noktanın, kristalin büyümeye başladığı orijinal çekirdeğin bulunduğu yer olduğu kabul edilebilir. Herhangi bir yüzün büyüme hızı kristalin merkezinden, yüze dik bir yönde yüzeyin geçiş hızıyla ölçülür. Kristal muntazam bir polihedron olmadıkça invaryant bir kristalin çeşitli yüzlerinin büyüme hızları eşit olmaz.

Şelil-1: İnvaryant bir kristalin büyümesi

Kristal Boyutu ve Biçim (Şekil) Faktörleri: Herhangi bir biçimdeki invaryant bir kristalin boyutunu ölçmek için tek bir boyut kullanılabilir. Bir kristalin toplam yüzey alanının (s_p), kristal hacmine (v_p) oranı,

s_p     6
¾ = ¾¾                      (1)
v_p   F_s D_p

F_s = küreselliktir. Bir kristalin karakteristik uzunluğu L, F_sD_p’ye eşit olarak tanımlanırsa,

               6 v_p
L = F_s D_p ¾¾              (2)
                s_p

küpler ve küreler için F_s = 1 ve L = D_p’dir. Geometrik katılar için, genellikle L, taramayla tayin edilen boyuta yakındır.

İnvaryant büyüme kavramı kristalizasyon prosesinin analizinde yararlıdır. Hatta pek çok kristalizörde koşulların ideallikten ve büyümenin invaryantlıktan uzak olduğu durumlarda bile kullanılabilir. Olağanüstü durumlarda bir yüz, diğerlerinin herhangi birinden çok daha hızla büyüyebilir ve uzun iğnemsi kriskaller oluşmasına yol açar. Bir yüz’ün yavaş büyümesi ise ince-levha veya disk-biçimli kristallerin (sulu çözeltide buz gibi) meydana gelmesine neden olur. Disk-biçimli kristaller için F_s oldukça düşük olabilir ve bu durumda uzunluk L’nin önemi kalmaz (Denklem-2). D_p boyutundaki diskler, L = F_s D_p boyuttaki bölmeyi geçemez.

 2. KRİSTALİZASYONUN PRENSİPLERİ

Kristalizasyon saflık, verim, enerji gereksinimleri, çekirdeklenme ve büyüme bakış açılarıyla analizlenebilir.

Ürün Saflığı: İyi oluşan bir kristal tamamen saflığa yakın bir formdadır. Ancak son magmadan* çekildikten sonra ana sıvıyı tutar, dolayısıyla çok az safsızlık içerir. Pratikte kristalde kalan ana sıvı süzme veya santrifüjle uzaklaştırılır, temiz solventle yıkanır. Bu saflaştırma aşamaları kristalin boyutu ve düzenliliğine bağlı olarak yapılır. (*Magma: ana sıvı ve çeşitli boyutlardaki kristallerin iki-fazlı karışımı)

Denge ve Verimler

Kristalizasyon prosesinde çözelti doygun hale geldiğinde dengeye ulaşılır; kütle (bulk) kristaller için denge ilişkisi çözünürlük eğrisidir. Çok küçük kristallerin çözünürlüğü, normal boyutlarda olanlara kıyasla daha büyüktür. Çözünürlük verileri standart tablolarda verilmiştir. Şekil-2’de sıcaklığın fonksiyonu olarak çözünürlük eğrileri görülmektedir. Pek çok malzeme, KNO₃ (1) eğrisine benzer eğriler verir; çözünürlükleri sıcaklıkla az veya çok artar. Az sayıda substans, NaCl (2)’ye benzer eğriler izler; sıcaklıkla çözünürlük çok az değişir.

Şekil-2: Sulu çözeltide, (1) KNO₃, (2) NaCl ve 

(3) MnSO₄.H₂O için çözünürlük eğrileri

Bazıları ise ‘ters (inverted) çözünürlük eğrisi’ olarak tanımlanan, sıcaklığın artmasıyla çözünürlüğün azaldığı bir yol izler; Şekilde (3) numaralı MnSO₄.3H₂Oeğrisi gibi.

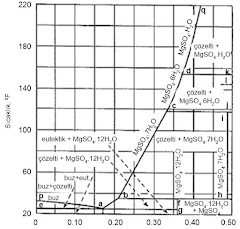
Pek çok inorganik bileşik, kristalizasyon suyu ile kristallenir (hidratlar). Bazı sistemlerde birkaç farklı hidrat oluşur; bu durum konsantrasyon ve sıcaklığa, komplike sistemlerde faz dengesine bağlıdır. Örnek olarak magnezyum sülfat-su sistemi için faz diyagramı Şekil-3’de verilmiştir. Diyagramda susuz magnezyum sülfatın (kütle fraksiyonu) konsantrasyonuna karşı denge sıcaklığı (⁰F) verileri görülmektedir. Yukarıdaki ve kırık hattın soluna doğru olan tüm alan, suda magnezyum sülfatın doygunluk altındaki çözeltilerini tanımlar.

·         eagfhij kırık hat, çeşitli katı fazlar oluşturan sıvı çözeltinin komple katılaşmasını gösterir.

·         pae alanı buz ve doygun çözelti karışımına aittir. %16.5’dan daha az MgSO₄ içeren herhangi bir çözeltide, sıcaklık pa hattına ulaştığında buz meydana gelir.

·         abcdq kırık hattı çözünürlük eğrisidir. %16.5’dan daha konsantre bir çözelti soğutulurken, sıcaklık bu hatta ulaştığında katı oluşmasına yol açar.

·         a noktasında oluşan katıya ‘eutektik’ denir; buz ve MgSO₄.12H₂O karışımıdır.

·         a ve b arasında kristaller MgSO₄.12H₂O.

·         b ve c arasında katı faz MgSO₄.7H₂O (epsom tuz).

·         c ve d arasında kristaller MgSO₄.6H₂O.

·         d’nin üstünde MgSO₄.H₂O.

·         cihb alanında sistem dengededir, doygun çözelti ve kristalin MgSO₄.7H₂O içerir.

·         dkjc alanında karışım doygun çözelti ve kristal MgSO₄.6H₂O içerir.

·         qdk alanında karışım doygun çözelti ve MgSO₄.H₂O içerir.

Verimler: Endüstriyel kristalizasyon proseslerin çoğunda kristaller ve ana sıvı, dengeye ulaşılabilecek yeterli süre boyunca temastadır; ana sıvı, işlemin sonunda doygun hale gelir. Prosesin verimi, orijinal çözeltinin konsantrasyonu ve son sıcaklıktaki çözünürlüğünden hesaplanabilir. Proses sırasında hissedilir derecede buharlaşma oluyorsa, bunun bilinmesi önemlidir.

Kristal büyüme hızı yavaş olduğunda dengeye ulaşılması için oldukça uzun zamana gerek vardır. Böyle bir durumla özellikle, çözeltinin viskoz olması veya kristallerin kristalizörün tabanında birikmesi ve süperdoygun çözeltiyle temastaki kristal yüzeyinin azalması halinde karşılaşılır. Bu gibi hallerde son ana sıvı süperdoygun halde kalır ve gerçek verim, çözünürlük eğrisinden hesaplanan değerden daha küçük olur.

Şekil-3: MgSO₄.H₂O faz diyagramı

Kristaller susuzsa, solut faz solvent içermeyeceğinden verim hesabı basittir. Ürün (crop) kristalizasyon suyu içerebilir; böyle durumlar çözeltide tutulan solut için uygun olmayacağından, kristaller suyu dikkate alınmalıdır. Çözünürlük verileri genellikle, her 100 kısım toplam solventin kütlesi için susuz malzemenin kütlesi olarak, veya susuz solutun kütle fraksiyonu olarak verilir. Bu verilerde kristalizasyon suyu dikkate alınmamıştır. Hidratlaşmış solutların verim hesaplarının anahtarı, tüm kütle ve konsantrasyonların hidratlanmış tuz ve serbest suyla ifadesidir. 

ÖRNEK-1: %30 MgSO₄ ve %70 su içeren bir çözelti 60 ⁰F’a soğutuluyor. Soğutma sırasında toplam suyun %5’i sistemde buharlaşıyor. Orijinal karışımın kilogramı başına kaç kg kristal kristal elde edilir?

Çözüm: (Şekil-3’ten)

kristaller: MgSO₄.7H₂O
ana sıvının konsantrasyonu: %24.5 MgSO₄ ve %75.5 H₂O
1000 kg orijinal çözeltide toplam su: 0.70 x 1000 = 700 kg
buharlaşma: 0.05 x 700 = 35 kg
MgSO₄ molekül ağırlığı: 120.4
MgSO₄.7H₂O molekül ağırlığı: 246.5
yığındaki (batch) toplam MgSO₄.7H₂O: 1000 x 0.30 (246.5/120.4) = 614 kg
yığındaki (batch) serbest su: 1000 – 35 – 614 = 351 kg
100 kg ana sıvıdaki MgSO₄.7H₂O: 24.5 (246.5/120.4) = 50.16 kg
100 kg ana sıvıdaki serbest su: 100 – 50.16 = 49.84 kg
ana sıvıdaki MgSO₄.7H₂O: (50.16/49.84) 351 = 353 kg
son ürün (crop): 614-353 = 261 kg

 

Entalpi Dengeleri: Kristalizörlerde ısı dengesi hesaplamalarında kristalizasyon ısısı önemlidir. Bu, bir çözeltiden katı oluştuğunda çıkan gizli ısıdır (latent heat). Kristalizasyon ekzotermik bir olaydır, ve kristalizasyon ısısı sıcaklık ve konsantrasyonla değişir. Kristalizasyon ısısı, doygun bir çözeltide kristallerin absorbladığı ısıya eşittir; bu değer, büyük miktarda bir solventteki çözelti ısısından ve doygunken seyreltilen çözeltinin seyrelme ısısından hesaplanabilir. Çözelti ısıları ve seyrelme verileri vardır; bunlar, kristallerin ve çözeltilerin spesifik ısıları verileriyle birlikte entalpi-konsantrasyon grafiklerinin hazırlanmasında kullanılabilir.

MgSO₄ ve su sistemi için katı fazların entalpilerini gösteren bir H-x diyagramı Şekil-4’de görülmektedir. Bu diyagram Şekil-3’teki faz diyagramıyla uyumludur. Entalpiler Btu/lb olarak verilmiştir ve karışımdaki faz sayısından bağımsız olarak 1 lb toplam karışımı ifade eder.

      ·         pabcdq hattı üzerindeki alan; suda altdoygun (undersaturation) MgSO₄ çözeltilerinin entalpilerini gösterir.
·         eap alanı: buz ve donmuş MgSO₄ çözeltilerinin tüm denge karışımlarını ifade eder. n noktası 32 ⁰F’da buza aittir.
·         aeg izotermal (25 ⁰F) üçgen: katılaşmış eutektik veya kısmen katılaşmış eutektik MgSO₄.12H₂O kristalleriyle buzun tüm kombinasyonlarının entalpilerini verir.
·         abfg alanı MgSO₄.12H₂O kristalleri ve ana sıvı içeren tüm magmalar için entalpi-konsantrasyon noktalarını verir.
·         bhf izotermal (35.7 ⁰F) üçgen: MgSO₄.7H₂O’nun MgSO₄.12H₂O’ya transformasyonu gösterir; %21 MgSO₄,doygun çözeltisi, katı MgSO₄.7H₂O ve katı MgSO₄.12H₂O karışımlarını kapsar.
·         cihb: MgSO₄.7H₂O ve ana sıvının tüm magmalarına aittir.
·         cji izotermal (118.8 ⁰F) üçgeni: %33 MgSO₄,doygun çözeltisi, katı MgSO₄.6H₂O ve katı MgSO₄.7H₂O karışımlarını kapsar.
·         dljc: MgSO₄.6H₂O ve ana sıvının entalpilerini gösterir.
·         dkl izotermal (154.4 ⁰F) üçgeni: %37 MgSO₄,doygun çözeltisi, katı MgSO₄.H₂O ve katı MgSO₄.6H₂O karışımlarını kapsar.
·         qrkd alanı: MgSO₄.H₂O ile dengedeki doygun çözeltilerdir.

Şekil-4: MgSO₄.H₂O sistemi için entalpi-konsantrasyon diyagramı

ÖRNEK-2: Batch bir kristalizörde 120 ⁰F (48.9 ⁰C) sıcaklıkta %32.5’luk MgSO₄ çözeltisi, su-soğutmalı bir kristalizörde (batch) önemli seviyede buharlaşma olmaksızın, 70 ⁰F (21.1 ⁰C)’ye soğutulmaktadır. Ton kristal için çözeltiden ne kadar ısı uzaklaştırılmalıdır?

Çözüm: Başlangıç çözeltisiŞekil-4’deki 120 ⁰F izotermi üzerinde altdoygun-çözelti alaında 0.325 konsantrasyondaki noktadır. Bu noktanın 0.325 konsantrasyonda entalpi koordinatı -33.0 Btu/lb’dir. Son magma için nokta cihb alanında 70 ⁰F izotermi üzerindedir. Bu noktanın entalpi koordinatı -78.4’dür. Orijinal çözeltinin her 100 poundu için çözeltinin entalpi değişimi,

100 (33.0 – 78.4) = -4540 Btu

Bu, 4540 Btu/100 lb (1.06 x 10⁵ J/kg) ısı çıkışıdır.

Son slurynin (bulamaç) kristaller ve ana sıvı bazında paylaşımında ‘merkez-gravite prensibi’nden yararlanılır; buna göre, iki fazlı bir karışımda fazların kütleleri, konsantrasyonları arasındaki farkla ters orantılıdır. Şekil-4’de 70 ⁰F’daki izoterme uygulandığında ana sıvının konsantrasyonu 0.259, kristallerin 0.488 olarak bulunur. Kristallerin miktarı,

        0.325 – 0.259

100 ¾¾¾¾¾¾¾¾ = 28.8 lb/100 lb slury

        0.488 – 0.259

Her ton kristal için çıkan ısı:

(4540/28.8) 2000 = 315000Btu/ton (3.66 x 10⁵ J/kg)

Süperdoygunluk: Bir çözeltiden kristalizasyon, homojen bir karışım içinde yeni bir fazın yaratılmasıdır. Olay iki aşamada gerçekleşir. Birincisi kristal oluşmasıdır; buna çekirdeklenme prosesi denir. İkincisi ise kristalin büyümesidir. Her iki aşama için de yürütücü potansiyel süperdoygunluktur; doygun veya altdoygun (undersaturasyon) bir çözeltiden çekirdeklenme de kristal büyümesi de oluşamaz. Teorik

Süperdoygunluk, üç metottan biri veya daha fazlasıyla meydana getirilebilir. Solutun çözünürlüğü sıcaklık yükselmesiyle kuvvetle artarsa-çoğu inorganik tuzlar ve organik substanslarla olduğu gibi-sıcaklığın düşürülmesi ve soğutmayla doygun çözelti, süperdoygun hale dönüşür. Çözünürlük sıcaklığa bağlı değilse-bazı yaygın tuzlarla olduğu gibi-süperdoygunluğa, solventin bir kısmının buharlaştırılmasıyla ulaşılır. Ne soğutma ve ne de buharlaştırma istenmediği durumlarda-çözünürlük çok yüksek olduğu haller-süperdoygunluk, üçüncü bir komponent ilavesiyle yaratılabilir. Üçüncü komponent fiziksel etkileşimle orijinal solventle, solventin çözünürlüğünün hızla azaldığı karışık bir solvent oluşturur. Bu proses ‘tuzlama’ denir. Yaklaşık olarak tam bir çökelme istendiğinde, orijinal solutla etkileşerek çözünmeyen bir substans veren üçüncü bir komponent ilavesiyle yeni bir solut yaratılabilir. Buna ‘çöktürme prosesi’ denir. Üçüncü bir komponent ilavesiyle çok büyük süperdoygunluklar hızla elde edilebilir.

Süperdoygunluk Birimleri: Süperdoygunluk, kristalin kristalin büyüdüğü süperdoygun çözelti ve kristalle dengedeki bir çözeltinin arasındaki konsantrasyon farkıdır. İki faz hemen hemen aynı sıcaklıktadır. Konsantrasyon, ya solutun mol kesriyle (y) veya birim çözelti hacimdeki solut molü (c) ile tanımlanabilir. Faz sınırları boyunca sadece bir komponent transfer edilir. İki süperdoygunluk,

Dy º y - y_s                   (3)

Dc º c - c_s                    (4)

Dy = süperdoygunluk, solutun mol kesri
y = çözeltideki solutun mol kesri
y_s = doygun çözeltideki solutun mol kesri
Dc = molar süperdoygunluk, mol/hacim
c = çözeltideki solutun molar konsantrasyonu
c_s = doygun çözeltideki solutun molar konsantrasyonu

Denklem (3) ve (4) ile tanımlanan süperdoygunluklar Denklem (5)’teki ilişkidedir:

Dc = r_M y – r_s y_s           (5)

r_M çözeltinin yoğunluğu ve r_s doygun çözeltinin yoğunluğudur. Kristalizörlerde süperdoygunluk genel olarak küçük olduğundan r_M ve r_s eşit kabul edilir; her ikisi için de r_M değeri kullanılır.

Dc = r_M Dy                    (6)

Konsantrasyon oranı a ve fraksiyonal süperdoygunluk s:

       c           Dc       y            Dy

a º ¾ = 1 + ¾¾ = ¾ = 1 + ¾¾ º 1 + s           (7)

       c_s          c_s       y_s           y_s

100s = % süperdoygunluktur. Uygulamada <%2’ dir. 

Sıcaklık Farkının Etkisi: Çözünürlük sıcaklıkla önemli derecede değiştiğinde süperdoygunluk, konsantrasyon farkı yerine eşdeğer bir sıcaklık farkıyla verilir. Bu yürütücü potansiyeller arasındaki ilişki Şekil-5’de verilmiştir. Hattın üstündeki alan doymamış çözeltileri, altındaki alan süperdoygun çözeltileri gösterir. A noktası T_c sıcaklığında doymuş bir çözeltiye aittir; büyüyen kristallerin sıcaklığıdır. D noktası, T sıcaklığındaki süperdoygun çözeltiyi ifade eder. Kristal büyürken ısı çıktığından T_c T’den biraz büyüktür; dolayısıyla, kristalden sıvıya ısı transferi için DT_h kadar yürütücü kuvvet meydana gelir. Bu sıcaklık farkı, tipik olarak 0.01-0.02 ⁰C seviyesindedir. Süperdoygunluk a normal olarak bulk (kütle) sıcaklığına bağlıdır; E ve D noktalarında gösterildiği gibi, gerçek süperdoygunluktan biraz daha büyüktür.

Şekil-5: Süperdoygunluk ve sıcaklık potansiyelleri

B noktası, kristalin büyüdüğü süperdoygun çözelti ile aynı konsantrasyonda doymuş bir çözeltiyi gösterir; sıcaklığı T_s’dir, T_s > T. C noktası T_c sıcaklığını ve süperdoygun çözeltinin konsantrasyonuna eşit bir konsantrasyonu tanımlar.

Denklem (3) ve (4)’den süperdoygun potansiyel AC hattıyla gösterilmiştir. Eşdeğer sıcaklık hattı BC’dir. Çözünürlük eğrisinin AB bölümünün, AC hattının küçük konsantrasyonlarında doğrusal olduğu düşünülebilir; sıcaklık potansiyeli,

DT º T_s – T_c = k (y – y_s) = k Dy = k/r_M Dc           (8)

k = T – y hattının eğimi, r_M = molar yoğunluktur.

Sıcaklık potansiyeli bu nedenle, çözeltinin gerçek sıcaklığı T’den ve doygunluk sıcaklığı T_s’den hesaplanandan biraz daha azdır. DT_h çok küçük olduğundan T_s – T ve T_s – T_c genellikle önemsizdir.

Çekirdeklenme

Çekirdeklenme hızı, birim magma (veya katı-içermeyen ana sıvı) hacmi başına birim zamanda oluşan yeni partiküllerin sayısıdır. Bu değer kristal boyut dağılımını (CSD, crystal size distribution) kontrol eden ilk kinetik parametredir.

Kristalizörlerdeki Kristallerin Kökenleri (Orijinleri): Tüm partiküllerin kaynağı çekirdeklenme terimi altında sınıflandırılırsa, bir dizi çekirdeklenme olayı meydana gelebilir. Gerçekte, çekirdeklenme üç grup altında toplanabilir;

     1.     Yapay (spuryus) çekirdeklenme
2.     Birincil (primer) çekirdeklenme
3.     İkincil (sekonder) çekirdeklenme

Kristallerin orijini makroskopik yıpranma veya aşınmadır; gerçek çekirdeklenmeden daha çok ufalanmaya benzer. Sirküle magma kristalizörlerde dahili propeller çalkalayıcılar veya harici sirkülasyon pompaları bulunur. Bu hareketli parçalara çarpan yumuşak veya zayıf kristaller kırılır, yuvarlak köşeli ve kenarlı büyük küçük yeni kristtaller oluşur, ürünün kalitesi bozulur. Yıpranma süperdoygunluğa bağlı değildir.

Deneysel çalışmalarda kristalizasyon sistemine ‘tohumlar’ ilave edilir; bunlar yüzeylerinde çok sayıda küçük kristaller taşır. Küçük kristaller hemen yıkanarak alınır ve süperdoygun çözeltide büyürler; buna ‘ilk ıslah ‘başlangıç ıslahı (initial breeding)’ denir. Tohum kristallerin kullanılmadan önce kürlenmemesi için gerekli önlemler alınmalıdır.

Şekil-6: Büyüme rejimi örneklemesi

Yapay çekirdeklenme, geniş süperdoygunluklar veya zayıf magma sirkülasyonlarında oluşur. Kristallerin sonlarında iğnemsi anormal büyümeler görülür; bu oluşumlar esas kristale zayıf bağlarla eklenerek kristali koparır ve kalitesini bozar. Buna ‘iğne ıslahı (needle breeding)’ denir.

‘Kısıtlı veya kapalı büyüme’, orta derece süperduygunluklarda oluşa diğer bir kusurlu büyüme formudur. Nedeni, anasıvının kristal yüzeyi içinde sıkışmasıdır; sütlü görünümlü, saf olmayan bir formdur.

Şeki6 ve Şekil-7 MgSO₄.7H₂O için çeşitli büyüme formlarını ve çekirdeklenme tipi ve kristal büyümesinde süper doygunluğun etkisi gösterilmiştir.

Şekil-7: MgSO₄.7H₂O için çekirdeklenme tipi ve kristal büyümesi

 üzerinde süper doygunluğun etkisi

Primer Çekirdeklenme: Bilimsel uygulamalarda çekirdeklenme, mevcut süperdoygun homojen bir faz içinde yeni bir fazda çok küçük oluşumların (body) doğmasıdır. Temel olarak çekirdeklenme fenomeni, çözeltiden kristalizasyon, bir ergiyikten kristalizasyon, aşırısoğumuş bir buharda sis damlalarının kondensasyonu, süperısınmış bir sıvıda kabarcıklar meydana gelmesiyle aynı olaydır. Her durumda çekirdeklenme, metastabil dengedeki homojen bir fazda hızlı bir dalgalanmanın (moleküler skalada) sonucudur; buna ‘homojen çekirdeklenme’ denilmektedir.

Farklı bir çekirdeklenme prosesi, ‘heterojen çekirdeklenme’ prosesidir. Değişik substansların katı partiküllerinin çekirdeklenme prosesini katalizleyerek çekirdeklenme hızını artırdığı bir prosestir.

Homojen Çekirdeklenme: Çözeltiden kristalizasyonda, bazı çökelme reaksiyonları hariç, homojen kristalizasyon hemen hemen hiç gerçekleşmez. Ancak çekirdeklenme tiplerini anlayabilmek için çekirdeklenme olayının temellerinin anlaşılması önemli ve gereklidir.

Kristal çekirdekleri çeşitli partiküllerden oluşabilir; moleküller, atomlar veya iyonlar gibi. Bunlar sulu çözeltilerde hidratlanabilir. Hareketleri rastgele olduğundan, bu partiküllerin birkaç tanesi küçük bir hacimde ‘cluster (küme)’denilen yapılaşma oluşturabilir; bunlar, kolayca kaybolan zayıf birleşmelerdir (agregasyon). Yeterli sayıda partiküller biraraya geldiğinde ise ‘embriyo’ olarak tanımlanan bir yapıda toplanabilir; bu durum bir latis düzeninin başlangıcı olup, yeni ve ayrı bir fazın oluşumuna yol açar. Çoğu koşulda embriyoların yaşam süresi kısadır ve clusterlere veya bireysel partiküllere dönüşür. Ancak süperdoygunluğun yeteri kadar büyük olduğu hallerde bir embriyo, çözeltiyle termodinamik dengeye gelebilecek bir boyuta kadar büyüyebilir; buna ‘çekirdek’ denilmektedir. Çekirdek, en küçük partiküller topluluğudur, içerdiği partiküller birbirlerinden ayrılmaz; bir kristal oluşturacak şekilde büyüyebilir. Kararlı bir çekirdek için gerekli partikül sayısı birkaç taneden yüzlerce taneye kadar değişebilir. Sıvı su için bu sayı 80 dolayındadır.

Çekirdekler kararsız bir denge halindedir: birimlerini kaybeden bir çekirdek çözünürken, yeni birimler kazanan bir çekirdek kristal forma dönüşür. Buna göre bir kristalin oluşum aşamaları aşağıda gösterildiği şekilde tanımlanabir:

Cluster¾® Embriyo ¾®  Çekirdek ¾®  Kristal

Denge: Termodinamik olarak, aynı sıcaklıkta küçük ve büyük bir partikül arasındaki fark, yüzey enerjisidir (birim kütle için); küçük partikülde önemli miktarda yüzey enerjisi olduğu halde, büyük partikülde yoktur. Bu durumun bir sonucu, küçük bir kristalin (mikrometre boyutundan daha küçük) çözünürlüğünün, büyük bir kristalden daha büyük olmasıdır. Genel çözünürlük verileri sadece orta derece büyüklüklerdeki kristallere uygulanabilir. Küçük bir kristal aşırıdoygun (süperdoygun) bir çözeltiyle denge halinde bulunabilir. Böyle bir denge kararsızdır; çünkü çözeltide büyük bir kristalin de bulunması halinde küçük olan kristal çözünecek ve tamamen yok oluncaya kadar büyük olan büyüyecektir. Bu fenomen ‘Ostwald Ripening (Ostwald Olgunlaşması)‘ olarak tanımlanır. Çözünürlükte partikül boyutunun etkisi, çekirdeklenmedeki anahtar faktörlerden biridir. 

Kelvin Eşitliği

Bir substansın çözünürlüğü partikül boyutuyla ilişkilidir; Kelvin eşitliğine göre,

          4V_M s

ln a = ¾¾¾                (9)

              n RTL

L = kristal boyutu
a = süperdoygun ve doygun çözeltilerin konsantrasyonlarının oranı
V_M = kristalin molar hacmi
s = katı ve sıvı arasındaki ortalama yüzeyarası gerilim
n = (iyonların sayısı) / (solut molekülü); moleküler kristaller için n = 1

a = 1 + s olduğundan, Denklem (9), süperdoygunluğu s olan çözeltiyle dengedeki kristallerin boyutunun (L), doygun çözeltiyle dengedeki büyük kristallere kıyasla, çok küçük olduğunu gösterir 

Çekirdeklenme Hızı: Kimyasal kinetik teorisinden, çekirdeklenme hızı aşağıdaki eşitlikle verilir:

                         16p V²_M N_a s³

B⁰ = C eksp [- -¾¾¾¾¾¾¾¾ ]            (10)

                       3(RT)³ v² (ln a)²

B⁰ = çekirdeklenme hızı, sayı/cm³-s
N_a = Avagadro sabiti, 6.0222.10²³ molekül/g.mol
R = gaz sabiti, 8.3143 x 10⁷ erg/g.mol-K
C = frekans faktörü

C faktörü, kritik boyuta ulaşan embriyoların oluşum hızının statistik bir ölçüsüdür. Bireysel partiküllerin konsantrasyonuyla ve kararlı bir çekirdek oluşturmak için gerekli kritik boyuttaki bir embriyoyla bu partiküllerin çarpışma hızıyla orantılıdır. Çözeltilerden çekirdeklenme için değeri bilinmiyor, ancak, aşırıdoygun su buharından su damlalarının oluşumunda (çekirdeklenme benzeşimi),

C »  10²⁵ çekirdek/cm³-s

dolayındadır. C faktörünün doğru değerinin bilinmesi önemli değildir; çünkü, çekirdeklenme kinetiğinde eksponentteki a terimi baskındır.

B⁰ eşitliğindeki s değeri de belirsizdir. Katı-sıvı yüzey arası gerilimlerin deneysel olarak saptanması zordur ve çok az veri mevcuttur. Latis (şebeke, örgü) enerjilerin kullanıldığı katı-hal teoriden tahminler yapılabilir. Sıradan tuzlar için s, 80-100 erg/cm²’dir. Denklem(10) da, yukarıdaki C ve s değerleri kullanıldığında s için bir değer hesaplanabilir. Bu değer bir çekirdeğin 1/(cm³ saniye) deki çekirdeklenme hızını gösterir, veya B⁰ = 1 dir. Hesaplanan s değeri çok büyüktür ve olağan çözünürlükteki malzemeler için mümkün değildir; bu nedenle, çözeltiden kristalizasyonda homojen çekirdeklenme asla meydana gelemez, bu koşullarda tüm gerçek çekirdeklenmeler heterojendir. Sonuç olarak Denklem(10) gerçek çekirdeklenme hızlarını vermez.

Çökelme reaksiyonlarında y_s çok küçük olduğundan, hızla aşırı doygunluk oranlarına ulaşılır ve homojen çekirdeklenme meydana gelebilir. 

Heterojen Çekirdeklenme: Katı partiküllerin, çekirdeklenme hızı üzerindeki katalitik etkisi, çekirdeklenme için gerekli enerjiyi düşürür. Bu etkiyle ilgili bir teoriye göre çekirdek katalistin yüzeyini ıslatıyorsa çekirdeğin oluşum işi, çekirdek ve katalist arasındaki açının fonksiyonu olan bir faktör kadar düşer. Potasyum klorür çözeltilerinin heterojen çekirdeklenmesiyle ilgili deneysel veriler, hem katalizlenmiş ve hem de katalist ilavesi olmadan çekirdeklenmeler için ‘görünür’ yüzeyarası gerilim değerinin 2-3 erg/cm² aralığında olduğunu göstermiştir. Katalist ilavesi olmadığı durumda, mikroskopik aşılarla self-katalizlenmiş ikincil bir çekirdeklenme gerçekleşiyorsa, aşılanmış KCl çözeltisi için s değeri, 300 K sıcaklıkta 2.8 erg/cm² olacaktır. Görünür yüzeyarası gerilim s_a ile gösterilerek, C = 10²⁵ olarak alındığında, matematiksel yaklaştırmayla küçük (a -1) değerleri için lna = a -1 = s kabul edilerek Denklem(10) aşağıdaki şekilde yazılır.

                           16p V²_M N_a s³_a
B⁰ = 10²⁵ eksp [- -¾¾¾¾¾¾¾]                     (11)
                             3(RT)³ v² s²

Bu eşitlik çekirdeklenmede süperdoygunluğun çok kuvvetli etkisini gösterir.

ÖRNEK-3: Potasyum klorürün heterojen çekirdeklenme hızının, 2.5 erg/cm² arayüzey gerilimiyle uyumlu olduğu kabul ediliyor. Çekirdeklenme hızını, 80 ⁰F (300 K) sıcaklıkta s’nin fonksiyonu olarak tayin ediniz.

Çözüm: Problemi çözümünde Denklem(11) kullanılır. KCl’ün molekül ağırlığı 74.56,. kristal yoğunluğu 1.988 g/cm³, disosiyasyonuyla K⁺ ve Cl^- iyonları oluşur; n = 2.

         74.56

V_M = -¾¾¾ = 37.51 cm³/g.mol      s_a = 2.5 erg/cm²

         1.988

Denklem (11)’de eksponent:

     16p (37.51)² x 6.0222 x 10²³ x 2.5³       0.03575

- -¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾ = - ¾¾¾¾

          3 (300 x 8.3143 x 10⁷)³ (2² s²)            s²

B⁰ = 1 için, s değeri:

1 = 10²⁵ e^-0.0357/s2 = e^57.565 e^-0.03575/s2
           0.03575/s² = 57.565      s = (0.03575/57.565)^1/2 = 0.02492
          B⁰ = e^57.565 e^-0.03575/s2

B⁰’nin 0.025 dolayındaki s büyüklüklerine göre hesaplanan değerleri Tablo-1’de toplanmıştır.

Tablo-1

s	B0	s	B0
0.023	4.47 x 10-5	0.0255	13.3
0.024	1.11 x 10-2	0.027	5.04 x 103
0.02492	1	0.029	3.46 x 106

ÖRNEK-4: 0.029 süperdoygunlukta dengedeki bir çekirdeğin, örnek-3’deki koşullar altında boyutu ne kadardır?

Çözüm: Problem Kelvin eşitliğiyle çözülür. Burada a = 1 + 0.029 = 1.029. Örnek-3’den V_M, s_a , v, R, T değerleri ile Denklem (9)’dan,

                     4 x 37.51 x 2.5

ln 1.029 = -¾¾¾¾¾¾¾¾¾¾¾

                2 x 8.3143 x 10⁷ x 300L

L = 2.63 x 10^-7 cm veya , 2.63 mm 

İkincil Çekirdeklenme: Çekirdeklenme oluşumu, magmada makroskobik kristallerin bulunmasından etkilendiğinde ‘ikincil çekirdeklenme’ söz konusudur. İki tür ikincil çekirdeklenme olabilir. Bunlardan biri akışkan-shear (makaslama) etkisiyle meydana gelir. Diğeri mevcut kristallerin birbirlerine, veya kristalizör duvarları, pervaneler veya çalkalayıcı kollarına çarpmalarıyla ilgilidir. 

Akışkan-Shear (Makaslama) Çekirdeklenme: Özel koşullar altında oluşan bir çekirdeklenme türüdür. Doygun çözelti, büyüyen bir kristalin yüzeyini geçecek şekilde uygun bir hızla hareket ettiğinde sınır tabakadaki shear gerilimler, embriyolar veya çekirdekleri süpürüp uzaklaştırır; aksi halde bunlar büyüyen kristalin içine girerek yeni kristaller oluşumuna neden olur. Böyle bir oluşum sakaroz kristalizasyonunda deneysel olarak saptanmıştır. Bu durum, MgSO₄ 7H₂O’nın çekirdeklenmesinin incelenmesi aşamalarında da kanıtlanmıştır: Çalışmada çözelti, kristal yüzeyinde bir aşırıdoygunlukta shear etkisindeyken hemen daha yüksek bir aşırıdoygunluğa hızla soğutulmuş ve çekirdeklerin makroskobik boyutlara büyümesine izin verilmiştir. 

Temas Çekirdeklenme: İkincil çekirdeklenmenin, çalkalanma şiddetinden etkilendiği uzun zamandan beri bilinmektedir; ancak, 1970’lere kadar bu etkinin yok edilmesiyle ilgili deneysel veriler elde edilememiştir. Temas çekirdeklenme endüstriyel kristalizörlerde en çok yapılan türdür, gerçekleşmesi için düşük aşırıdoygunlukta çalışılır. Koşullar, iyi kaliteli kristallerin büyüme hızı için optimum seviyede olmalıdır. Kristale çarpan enerji fevkalade düşüktür (birkaç yüz erg) ve kristal yüzeyinde görünür bir etki yapmaz. Çekirdeklenme ve kristal büyümesi alanlarında temas çekirdeklenmenin konumu Şekil-7’de noktalı hatlarla gösterilmiştir.

Bu konuda yapılan çalışmalarda, çarpmada darbe enerjisi bilinen küçük çubuklar ve akışkan aşırıdoygun bir çözeltide konumlanmış bireysel kristallerin seçilmiş yüzeyleri kullanılmış, oluşan çekirdeklerin sayısı ölçülmüştür: sayının, sadece aşırıdoygunluğa ve darbe enerjisine bağlı olduğu görülmüştür. İnorganik kristaller için, her N temastaki çekirdeklerin sayısı süperdoygunluk s ile, bazı organik kristaller için ln N, s ile orantılıdır. Organik ve hidratlanmış inorganik kristaller için N sayısının doğrudan temas enerjisi (E) aralığıyla orantılı olduğu görülmüştür; E, pratikte önemli bir parametredir, fakat susuz inorganik kristaller için gerekli enerji, diğer kristaller için olandan daha büyüktür ve çekirdeklenmeden önce bir eşik enerjiye ihtiyaç vardır. Daha yüksek temas enerjileri için N sayısı eksponensiyal E ile orantılıdır.

Peşpeşe yapılan temas denemeleri aynı çekirdeklenmeyi veriyorsa, temasların genellikle birkaç saniye aralıkla yapılması uygun bir yöntermdir.

Temas çekirdeklenme, büyüyen kristalin yüzeyi üzerinde mikroskopik dendritik oluşumların (büyümelerin) kırılmalarının ve kristal içinde organize olmak için hareket eden solut partikülleri clusterlerle temas eden objelerin arayüzünün bir kombinasyonu olabilir. Temas eden objelerin hareketinin, embriyolardan-L’den çok daha büyük küçük kristallere kadar olan boyuttaki partikülleri saptırıp çıkardığı varsayılıyor; yani, aşırıdoygun çözeltiyle dengede bulunan bir kristalin maksimum boyutu Kelvin eşitliğinde verildiği gibidir (Denklem-9). En az L kadar büyüklükteki partiküller yaşayabilir ve yeni çekirdekler olarak büyürken, daha küçükler çözünür.

Kristal Büyümesi

Kristal büyüme, büyümenin meydana geldiği katı yüzeylerin etkisiyle yönlendirilen bir difüzyon prosesidir. Solut moleküller veya iyonlar, sıvı faz boyunca difüzyon yoluyla bir kristalin büyüyen yüzeylerine ulaşır. Bu aşamaya klasik kütle-transfer katsayısı uygulanır. Yüzeye gelen moleküller ve iyonlar kristal tarafından kabul edilmeli ve uzamsal latiste organize edilmelidir. Yüzeyde sınırlı bir hızla meydana gelen reaksiyonla tüm proses iki kademede tamamlanır. Çözelti aşırıdoygun olmadıkça difüzyonal ve yüzeyarası kademeler gerçekleşemez. 

Bireysel ve Tüm Büyüme Katsayıları: Kütle transferi operasyonlarında fazlar arasındaki arayüzde denge olduğu kabul edilir. Kristalizasyonda böyle bir koşulda, kristalin yüzeyinde çözeltinin konsantrasyonu doygunluk değerindedir (y_s); kütle transferi için toplam yürütücü kuvvet y – y_s olacaktır (y, kristal yüzeyinden belli bir mesafedeki konsantrasyonur). Yüzey reaksiyonu nedeniyle, arayüzey kademesi için bir yürütücü kuvvete gerek vardır: arayüzeki konsantrasyon y’ ile gösteriliyor; y_s < y’ < y. Kütle transferi için yürütücü kuvvet y –y’ (Şekil-8).

Şekil-8: Kristalizasyonda sıcaklık ve konsantrasyon ilişkisi

Kütle transferi ve yüzey reaksiyonu katsayıları bir kristal yüzeyinden diğer bir kristale değişir, fakat tüm kristal için sadece ortalama değerler dikkate alınabilir.

Bu bakış açısıyla kütle transferi eşitliği,

        m^.
N_A = ¾ = k_y (y – y’)                   (12)
        s_p

NA = molar akı, mol/(zaman.alan)
m^. = kütle transfer hızı, mol/saat
s_p = kristalin yüzey alanı
k_y = kütle transfer katsayısı

Yüzey reaksiyonu için k_s değeri kullanılır ve tüm katsayı K eşitliği çıkarılır::

m^.
¾ = k_y (y’ – y_s)                         (13)
s_p

           m^.
K º ¾¾¾¾¾                            (14)
      s_p (y – y_s)

             1
K º ¾¾¾¾¾¾                         (15)
      1/k_y – 1/k_s)

 

Büyüme Hızı: Değişmeyen (invaryant) bir kristal için kristalin hacmi (v_p). karakteristik uzunluğunun (L) küpü ile orantılıdır.

v_p = a L³                                  (16)

a bir sabittir. r_M molar yoğunluk ise, kristalin kütlesi m:

m = v_p r_M = a L³ r_M                  (17)

Denklem (17) zamana göre.

        dm                      dL

m^. = ¾¾  = 3 a L² r_M (¾¾)                  (18)

         dt                       dt

Büyüme hızı dL/dt, G ile gösterilir. Aşağıda görülen Denklem 2’den,

                6 v_p

L = F_s D_p ¾¾

                s_p

s_p = 6 v_p/L = 6 a L²

Denklem (18) ve (14) kullanılarak, Denklem (19) ve bundan da (19) elde edilir.

       3 a L² r_M G

K = ¾¾¾¾¾¾¾                     (19)

       6 a L² (y - y_s)

      2 K (y – y_s)

G = ¾¾¾¾¾¾                         (20)

            r_M

 

Kütle-Transfer Katsayıları: Şekil faktörü 1.0’a yakın kristaller veya küreler için kütle transfer katsayısı k_y’yi tahmin etmek için,

N_Sh = 2.0 + 0.6 N_Re^1/2 N_Sc^1/3

Eşitliği kullanılabilir. Çalkalanan bir sistemde süspansiyon haldeki partiküller için kütle-transfer katsayısı, kristallerin uç ayar hızından hesaplanan değerin 1.5-5 katı kadardır.

 

Yüzey-Büyüme Katsayıları: Yüzeyarası reaksiyonla kristallerin büyümesiyle ilgili pek çok araştırma yapılmış ve standart monograflar yayınlanmıştır. Kristal büyümesiyle uyumlu bir teori geliştirilmiş olmasına rağmen dizaynda kullanılan, k_s hakkındaki sayısal veriler azdır.

Bir teori, büyümenin kristal yüzeyinde tabaka-tabaka oluştuğu kavramına dayanır; her yeni tabaka yüzeye eklenen iki boyutlu bir çekirdek gibi başlar. Bu teori büyümenin, uygun bir eşik süperdoygunluğa ulaşılıncaya kadar başlamayacağını ve süperdoygunlukta büyüme hızının hızla artacağını ve doğrusal (lineer) olacağını kabul eder. Gerçekte, pek çok kristalin büyüme hızı süperdoygunlukla lineerdir, bir eşik değerinin olması zorunluluğu yoktur.

Gözlenen ve teorik büyüme hızları arasındaki fark, Frank vida (screw)-çıkığı (dislokasyon) teorisiyle ilişkilendirilmiştir. Hakiki kristallerin gerçek uzam latisleri mükemmel değildir ve böyle kusurlu kristallere ‘dislokasyonlar’ denir; bunlarda yüzeylerde ve kristal içindeki partiküllerin düzlemleri yer değiştirir. Birkaç çeşit dislokasyon vardır. Çok bilinen bir dislokasyon vida-dislokasyondur (Şekil-9’da bireysel partiküller kübik yapı blokları olarak gösterilmiştir). Bir shear düzlemdeki dislokasyon kridtsl yüzeyine paraleldir ve kristalin kaymasıyla bir rampa meydana gelir. Rampanın kenarı iki-boyutlu bir çekirdek gibi davranarak içinde partiküllerin kolayca yerleşebileceği bir kıvrıntı hazırlar. Tam bir yüzey asla oluşmaz ve çekirdeklenme yoktur. Büyüme devam ederken rampanın kenarı spirale dönüşür, kenar boyunca devam eden partikül çökelmesi kristal büyüme mekanızmasını oluşturur. Böyle bir mekanizma ileri sürüldüğünden pek çok vida dislokasyon örnekleri, elektron Mikroskopisi ve diğer yüksek ileri teknoloji araçlarıyla incelenmiş ve gerçekliği gözlenmiştir.

Şekil-9: Kristal yüzeyinde vida çıkığı ve partikülün dolaşması

Kristal Büyümesi DL Kanunu: Magmadaki tüm kristaller, benzer bir süperdoygun alanda, aynı sıcaklıkta ve süperdoygunluğun yarattığı bir hızda doğarak büyürse, bunlar birbirinin aynısı olmakla kalmaz, boyuttan bağımsız aynı büyüme hızına sahip olurlar. Buna DL kanunu denilmektedir.

G ¹ f(L)  uygulandığında,

Magmadaki her kristalin, aynı zaman aralığında (Dt) toplam büyümesi aynıdır.

DL = G Dt                                 (21)

Denklem(21) deki model son derece ideal bir hali gösterir; ancak tüm koşullarda gerçekçi değildir. Partikül çaplarının sadece sınırlı bir aralığında kütle transfer katsayısı yaklaşık olarak sabittir; kütle transfer direnci önemli seviyelerde olduğunda sabit bir büyüme hızı, sadece 50-100 mm arasındaki boyutlarda kristaller için beklenebilir. Denklem(21) uygulanamadığında, G = f(L) ve büyüme ‘boyut bağımlı’ olarak tanımlanır. Hataların iptal edilmesiyle DL kanunu pek çok durumda yeterli olabilir ve endüstriyel proseslerde hesaplamaları önemli derecede basitleştirir.

3. KRİSTALİZASYON CİHAZI

Ticari kristalizörlerde ya sürekli (komtinü) veya yığın (batchwise) yöntemi kullanılabilir. Özel uygulamalar dışında sürekli yöntem yercik edilir. herhangi bir kristalizör için ilk gereksinim süperdoygun bir çözeltinin oluşturulmasıdır; çünkü, süperdoygunluk olmadan kristalizasyon oluşamaz. Süperdoygunluğun (aşırıdoygun) sağlanabilmesi için, solutun çözünürlük eğrisinin yapısına bağlı olarak uygulanan üç metot vardır:

1. Potasyum nitrat ve sodyum sülfit gibi solutlar düşük sıcaklıklarda, yüksek sıcaklıklara göre çok daha az çözünürler; bu nedenle soğutmayla süperdoygunluk kolaylıkla sağlanabilir.

2. Çözünürlüğün sıcaklığa hemen hemen bağlı olmadığı -sıradan tuzlar gibi- veya sıcaklığın artmasıyla azaldığı durumlarda süperdoygunluk buharlaştırmayla yaratılır.

3. Ara hallerde hem buharlaştırma ve hem de soğutma kombinasyonu etkindir. Örneğin sodyum nitrat, buharlaşma olmadan soğutularak, soğutma olmadan buharlaştırılarak, veya bir soğutma-buharlaştırma kombinasyonuyla başarıyla kristallendirilebilir.

Kristalizörlerdeki Değişiklikler: Ticari kristalizörler, çeşitli yöntemlerle farklılaştırılabilir. Önemli bir farklılık, kristallerin süperdoygun sıvıyla nasıl temas ettirileceği ile ilgilidir.

Birinci teknikte süperdoygun bir çözelti akımı, büyüyen kristallerin akışkan yatağından geçirilir, süperdoygunluk çekirdeklenme ve büyümeyle harcanır; bu yöntem ‘sirkülasyon-sıvı metot’ olarak adlandırılır. Doygun sıvı sonra bir soğutma veya buharlaştırma bölgesine pompalanır, burada tekrar süperdoygun hale getirilir ve son olarak da kristalizasyon bölgesinde resaykıla (geridönüşüme) alınır.

İkinci teknik, ‘sirkülasyon-magma metodu’dur. Bu yöntemde magmanın tümü, sıvı katıdan ayrılmaksızın, hem kristalizasyon ve hem de süperdoygunluk aşamalarında sirküle edilir. Mevcut kristallerde, kristalizasyon ve süperdoygunluk metdana gelir.

Her iki metotta da, kristallenme ve süperdoygunluk bölgeleri arası sirkülasyon akımına besleme çözeltisi ilave edilir.

Kristalizörlerin bir tipinde boyut-sınıflandırma cihazları kullanılır; bu cihazlar büyüme bölgesinde, daha fazla büyüyebilmesi için küçük kristallerin kalmasına, ürün olarak sadece belirtilen minimum boyutlardaki kristallerin geçmesine izin verecek şekilde dizayn edilir. İdeal hal, böyle bir kristalizörün ‘tek uniform boyutta’ sınıflandırılan bir ürün vermesidir. Diğer kristalizörler, kristallenme bölgesinde tamamen karıştırılan-süspansiyonlar bulunacak şekilde dizayn edilir; çekirdekten-büyük kristallere kadar tüm boyuttaki kristaller muntazam olarak magma boyunca dağılmıştır. İdeal olanı, bir karıştırma süspansiyon ünitesinden alınan üründe boyut dağılımının magmadaki kristallenmeye eşdeğer olmasıdır.

Bir karıştırılan-süspansiyon ünitesinden alınandan daha büyük boyutta ortalama kristal boyutu elde edebilmek için, bazı kristalizörlerde, kristalizasyon bölgesinden ince kristallerin çoğunu ayırıp uzaklaştıran cihazlar bulunur. Bu küçük kristaller tekrar çözülür ve kristalizöre gönderilir. Diğer bir tip kristalizörlerde iki ‘take-off (çıkarma)’ hattı bulunur; bunlardan biri büyük kristaller, diğeri küçükler içindir. Hacimleri oldukça farklı iki ürün akımı birleştirilir ve bir filtreye veya ayırma ünitesine verilir.

Kristalizörlerin çoğunda, büyüme hızını geliştirmek, süperdoygun çözeltinin ayrılmasını önlemek (fazla çekirdeklenmeye neden olur) ve kristalleri kristalizasyon bölgesinde süspansiyon halde tutabilmek için çeşitli çalkalama formları kullanılır. Çoğu zaman çekme-tüpleri ve bafıllarla teçhiz edilmiş dahili pervane çalkalayıcılar kullanılabilir. Kristalizasyon bölgeleri veya süperdoygunluk boyunca sıvı veya magmanın sirkülasyon için harici pompalar da çok kullanılır; bu metoda ‘zorlamalı (forced)-sirkülasyon’ denir. Dıştan ısıtıcılı zorlamalı-sirkülasyonun ünitelerinin bir avantajı, birkaç aynı ünitenin birleştirilerek bir üniteden alınan buharın hattaki diğer birini ısıtmada kullanılabilmesidir; bu tip sistemlere ‘buharlaştırıcı-kristalizörler’ denilmektedir. 

Vakum Kristalizörler: Vakum üniteleri sınıfındaki en modern kristalizörlerdir; bunlarda süperdoygunluk yaratılması, adyabatik buharlaştırmayla sağlanır. Orijinal ve en basit formunda böyle bir kristalizör vakum altında kapalı bir kaptır, kristalizör ve bir kondenser arasına konulan bir buhar-jet vakum pompasıyla sürekli bir vakum sağlanır. Sisteme (kap), kristalizörün basıncında, kaynama noktasının üzerindeki bir sıcaklıkta (genellikle ılık olur) doygun bir çözelti beslenir. Magma hacmi, kaptaki kristallenen katı ve sıvı seviyesi tarafından kontrol edilir; magmanın üstündeki boşluk buharın çıkarılması ve sürüklenenlerin giderilmesinde kullanılır. Besleme çözelti denge sıcaklığına kendiliğinden soğur. Çünkü hem soğuma entalpisi ve hem de kristalizasyon entalpisi, buharlaşma entalpisi haline dönüşür; solventin bir kısmı buharlaşır. Soğuma ve buharlaşmayla oluşan süperdoygunluk çekirdeklenme ve büyümeyi sağlar. Magma ürünü kristalizörün dibinden çekilir. Kristallerin teorik verimi, denge sıcaklığında solutun çözünürlüğü ve beslemenin konsantrasyonu arasındaki farkla orantılıdır. Şekil-10’da, yardımcı ünitelerin, magma ürün ünütesi ve işlenmesinin de yer aldığı bir sürekli vakum kristalizörün şematik görünümü verilmiştir.

Şekil-10: Sürekli bir kristalizörün şematik görünümü

Draft Tüp-Bafıl Kristalizör: Çok yönlü ve etkin bir ekipman olan draft tüp-bafıl (DTB) kristalizör Şekil-11’de görülmektedir. Kristalizör cihazında, aynı zamanda  magmanın sirkülasyonunu kontrol eden bafıl (bölme) gibi davranan bir draft (çekme) tüp ve kontroledilebilen bir sirkülasyon sağlayan aşağı-yönlü bir propeller çalkalayıcı  bulunur. kristalizörün dışında ilave bir sirkülasyon sistemi vardır; bir sirkülasyon pompasıyla çalıştırılır, ısıtıcı ve besleme girişi içerir. Slury (bulamaç) ürün kristalizörün konik alt kısmından uzaklaştırılır. Verilen bir besleme hızı için içteki ve dıştaki sirkülasyon sistemleri bağımsız olarak çalıştırılarak istenilen CSD (crystal size distribution) kontrol altında tutulur.

Draft tüp-bafıl kristalizörlerde, kristalleri boyutlarına göre sınıflandırma ve inceleri ayırma amaçlı bir elutriasyon (yıkayıcı) bacak bulunur (Şekil-12). Sirkülasyondaki sıvının bir kısmı bacağın altına pompalanır ; küçük kristalleri, daha fazla büyüyebilmeleri için tekrar kristalizasyon bölgesine taşır.

Şekil-11: Draft  tüp-bafıl (DTB)

 

Şekil-12: Draft tüp-bafıl kristalizör; inceleri ayırma ve uzaklaştırma için dahili sistem içeriyor

ÖRNEK-5: sürekli çalışan bir vakum kristalizöre %31’lik MgSO₄ çözeltisi beslenmektedir. Kristalizörde magmanın denge sıcaklığı 86 ⁰F (30 ⁰C) ve çözeltinin kaynama noktası yükselmesi 2 ⁰F (1.11 ⁰C)’dir. Saatte 5 ton (4536 kg) MgSO₄ 7H₂O magma ürün elde edilmektedir. Katının magmaya hacim oranı 0.15, kristallerin ve ana sıvının yoğunlukları 105 ve 82.5 lb/ft³’tür. Beslemenin sıcaklığı, besleme hızı ve buharlaşma hızı nedir?

Çözüm: Problemin grafiksel çözümü Şekil-13’te gösterilmiştir.

Şekil-13: Örnek 5’in çözümü için

 

Buhar, kristalizörü 84 ⁰F sıcaklığın karşılığı olan basınçta terk eder, 2 ⁰F aşırı ısı taşır (bu ihmal edilebilir). Buhar tablolarından, buharın entalpisi 0.5771 lb_f/in² ve,

a noktasının koordinatları: H = 1098 Btu/lb  c = 0

Ürün magmanın ortalama konsantrasyonu ve entalpisi Şekil-4’deki verilerden hesaplanır. fd hattı, Şekil-4’deki bcih alanındaki 86 ⁰F izotermidir. Uçların koordinatları,

f noktasının koordinatları: H = -43 Btu/lb  c = 0.285
          d noktasının koordinatları: H = -149 Btu/lb  c = 0.488

Kristallerin ana sıvıya kütle oranı:

 0.15 x 105

¾¾¾¾¾¾ = 0.224

0.85 x 82.5

Ana sıvının üretim hızı: 10 000/0.224 = 44520 lb/saat
          Üretilen toplam magma: 10 000 + 44520 = 54520 lb/saat

Magmadaki ortalama MgSO₄ konsantrasyonu:

0.224 x 0.488 + 0.285
¾¾¾¾¾¾¾¾¾¾¾¾ = 0.322

                1.124

Magmanın entalpisi:

 0.224 (-149) + (-43)
¾¾¾¾¾¾¾¾¾¾¾ = - 62.4 Btu/lb

              1.124

Bunlar e noktasının koordinatlarıdır. Besleme noktası ae hattı üzerinde olmalıdır. Besleme konsantrasyonu 0.31 olduğundan, beslemenin entalpisi b noktasının ordinatı veya -21 Btu/lb’dir. b noktası 130 ⁰F (94.4 ⁰C) izotermi üzerindedir ve dolayısıyla bu sıcaklık besleme sıcaklığıdır.

Merkez-gravite prensibine göre buharlaşma hızı,

          -21 – (-62.4)
54520 ¾¾¾¾¾¾¾ = 2017 lb/saat (915 kg/saat)

           1098 - (-21)

Toplam besleme hızı:

54520 + 2017 = 56537 lb/saat (25645 kg/saat) 

Organik Kimyasalların Kristalizasyonu: Bu bölümdeki tüm örnekler inorganik tuzlarla ilgilidir. Çözeltiden kristalizasyondaki ilkeler organık malzemelere de uygulanabilir. Walas, literatürde bazı organik bileşiklerin kristalizasyon verilerini listelemiştir. Organik bileşikler ‘Ergiyik (Melt) Kristalizasyon’ yöntemiyle de saflaştırılabilir.

4. ERGİYİKLERDEN (MELT) KRİSTALİZASYON

Bazı organik bileşiklerin yapılmasında son aşama ürünün, saflaştırılmış bir ergiyik akımdan katılaştırılmasıdır. Bu işlem genellikle, dondurularak (drum flakerde) veya soğutularak (titreşimli konveyörde) veya çalkalanarak (ceketli çalkalama kabında) yapılır. Bazen sıvı dondurmadan 20-50 ⁰C kadar soğutulabilir ve mekanik çalkalama veya aşılamayla kristalizasyon başlatılabilir.

İkili veya üçlü organik karışımlar, özellikle aromatik izomerler basit soğutmalarla saflaştırılabilir. Katı çözeltiler oluşmadıkça çoğu zaman, bir izomerin gerçek saf kristalleri üretilebilir. Örneğin, ksilen izomerlerin karışımı iki-kademeli bir kristalizasyon sisteminde -60 ⁰C’de işlemlendiğinde p-ksilen kristaller ayrılır; ilk oluşan kristaller yeteri kadar saf değildir, ergitilir ve yeniden kristallendirilir. İkinci ürün toluen veya başka uygun bir solventle yıkanarak yapışmış olan ana sıvı uzaklaştırılır.

Diğer işleme sistemlerinde saf ürün ergitilir, bir kısmı, kristallerin yıkanması ve saflaştırılması için refluks edilir. Böyle tipe bir örnek olarak, Şekil-14’te görülen ‘Brodie Saflaştırıcı’ gösterilebilir. Sistemde, yerleştirilmiş birkaç pürüzlü-yüzeyli soğutucu serisi ve saflaştırma kolonunu bulunur. Ergimiş besleme son suğutucunun ortasından girer. Sıvı, sistemin sıcaklığın en düşük olduğu kalıntı uçuna doğru akar. Kristaller konveyörler tarafından ürün tarafına taşınır, dikey saflaştırma kolonuna boşaltılır. Kolonun tabanında ergitilen kristallerin bir kısmı ürün olarak çekilir, bir kısmı da kolonun üstünden refluks edilir. Refluks, kristal yüzeylerini yıkar, kalıntıları temizler, ergime noktalarına getirir. Bu yöntemle klorobenzen izomerlerden % 99.9 saflıkta p-diklorobenzen elde edilmiştir.

Şekil-14: Brodie Saflaştırıcı karşıakım soğutmalı kristalizör

9 Şubat 2021

 

GERİ (proje çalışmaları)