Prof. Dr. Bilsen Beşergil: Kuantum Mekaniği (quantum mechanics)

Kuantum mekaniği; madde ve ışığın, atom ve atomaltı seviyelerdeki davranışlarını inceleyen bilim dalıdır; nicem mekaniği veya dalga mekaniği adlarıyla da anılır. Kuantum mekaniği; moleküllerin, atomların ve bunları meydana getiren elektron, proton, nötron, kuark, gluon gibi partiküllerin özelliklerini açıklamaya çalışır. Çalışma alanı, partiküllerin birbirleriyle ve ışık, X-ışını, gama ışını gibi elektromagnetik radyasyonlarla olan etkileşimlerini de kapsar.

Kuantum mekaniğinin temelleri 20. yüzyılın ilk yarısında Max Planck, Albert Einstein, Niels Bohr, Werner Heisenberg, Erwin Schrödinger, Max Born, John von Neumann, Paul Dirac, Wolfgang Pauli gibi bilim adamlarınca atılmıştır. Belirsizlik ilkesi, anti madde, Planck sabiti, kara cisim ışınımı, dalga kuramı, kuantum alan kuramı gibi kavram ve kuramlar bu alanda geliştirilmiş ve klasik fiziğin sarsılmasına ve değiştirilmesine neden olmuştur.

Kuantum kuramına göre partiküller 3 konum ve 3 momentumla tanımlanmak yerine bir ‘dalga fonksiyonu’ ile tanımlanır. Dalga fonksiyonu ‘olasılık fonksiyonu’ olarak anılır.

Konum-uzay dalga fonksiyonları

Böyle bir partikülün durumu, dalga fonksiyonu ile tamamen tanımlanır.

Ψ(x, t)

X: konum, t: zamandır. Bu, iki gerçek değişken x ve t'nin karmaşık değerli bir işlevidir.

|Ψ (x, t)|² = Ψ (x, t)* Ψ (x, t)| = r(x, t)

Bu eşitlik partikülün x'de bulunma olasılığı (yoğunluğu) olarak yorumlanır. Yıldız işareti, karmaşık eşleniği gösterir.

Partikülün konumu dalga fonksiyonundan belirlenemez, ancak olasılık dağılımı ile tanımlanır. x pozisyonunun a ≤ x ≤ b aralığında olması ihtimali, bu aralıktaki yoğunluğun integralidir:

P_a≤x≤b (t) = ∫ dx |Ψ(x, t)|²

Bu eşitlik normalizasyon koşulunu verir. Çünkü partikül ölçülürse, bir yerde olma olasılığı% 100'dür.

∫ dx |Ψ(x, t)|² = 1

-¥

Sonuç olarak Ψ₁ ve Ψ₂ dalga fonksiyonları için aşağıdaki eşitlik yazılır.

(Ψ₁, Ψ₂) = ∫ dx Ψ₁*(x, t) Ψ₂(x, t)

-¥

Momentum-uzay dalga fonksiyonları

Partikül momentum uzayında da bir dalga fonksiyonuna sahiptir.

F(p, t)

p: bir boyuttaki momentum (-∞ ile +∞ arasında bir değer olabilir), t: zamandır.

Konum durumuna benzer olarak aşağıdaki eşitlik yazılır:

(F₁, F₂) = ∫ dp F₁*(p, t) F₂(x, t)

-¥

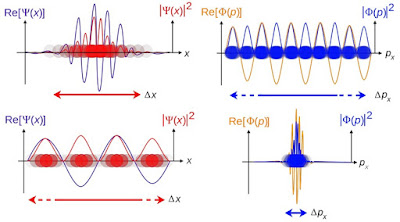
Serbest bir partikülün hareket dalgaları: x veya p boyutundaki bir spin-0 partikülü için konum dalga fonksiyonu Ψ(x) ve momentum dalga fonksiyonunu Φ(p), ve karşılık gelen olasılık yoğunlukları |Ψ(x)|₂ ve |Φ(p)|₂.

https://en.wikipedia.org/wiki/Wave_function

https://tr.wikipedia.org/wiki/Kuantum_mekani%C4%9Fi

27 Ağustos 2019

GERİ (yasalar)

GERİ (astrofizik)

GERİ (koruma yasaları)
GERİ (fizik anasayfa)
GERİ (kimya anasayfa)