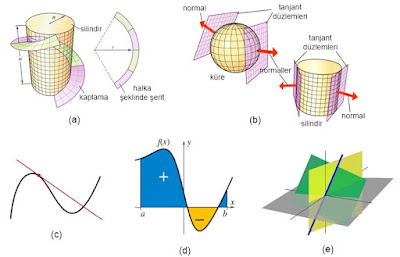
Diferansiyel geometri, düzgün manifoldlar olarak da bilinen düzgün şekillerin ve düzgün uzayların geometrisini inceleyen bir matematik disiplinidir; diferansiyel hesap, integral hesap, doğrusal cebir ve çoklu doğrusal cebir tekniklerini kullanır.
Alanın kökenleri, antik çağlara kadar uzanan küresel geometri
çalışmalarına dayanmaktadır. Aynı zamanda astronomi, Yer'ın jeodezisi ve daha
sonra Lobaçevski'nin hiperbolik geometri çalışmasıyla da ilgilidir. Pürüzsüz
uzayların en basit örnekleri, üç boyutlu Öklid uzayındaki düzlem ve uzay
eğrileri ve yüzeyleridir; bu şekillerin incelenmesi, 18. ve 19. yüzyıllarda
modern diferansiyel geometrinin gelişiminin temelini oluşturmuştur. 19.
yüzyılın sonlarından bu yana diferansiyel geometri, daha genel olarak
diferansiyellenebilir manifoldlardakigeometrik yapılarla ilgilenen bir alan
haline geldi.
Bir geometrik yapı, bazı boyut, mesafe, şekil, hacim ve diğer sabitleştirme kavramlarını tanımlayan yapıdır. Örneğin,
Riemann geometrisinde mesafeler ve açılar belirtilir, simplektik geometride
hacimler hesaplanabilir, konformal geometride yalnızca açılar belirtilir, ayar
teorisinde uzay üzerinde belirli alanlar verilir.
Diferansiyel geometri, herhangi bir ek geometrik yapıya dayanmayan
diferansiyellenebilir manifoldların özellikleriyle ilgilenen diferansiyel
topoloji ile yakından ilişkilidir ve bazen onu içerdiği kabul edilir.
Diferansiyel geometri aynı zamanda geometrik analiz olarak da bilinen
diferansiyel denklemler teorisinin geometrik yönleriyle de ilgilidir.
Diferansiyel geometri matematik ve doğa bilimlerinde uygulama alanı
bulur. Diferansiyel geometrinin dili en belirgin şekilde Albert Einstein
tarafından genel görelilik teorisinde ve daha sonra fizikçiler tarafından
kuantum alan teorisinin ve standart partikül fiziği modelinin geliştirilmesinde
kullanıldı. Diferansiyel geometri, fiziğin dışında kimya, ekonomi, mühendislik,
kontrol teorisi, bilgisayar grafikleri ve bilgisayar görüntüsü, ve son
zamanlarda makine öğreniminde de uygulama alanı bulmaktadır.
https://en.wikipedia.org/wiki/Differential_geometry
22 Ocak 2024
GERİ (matematik anasayfa)