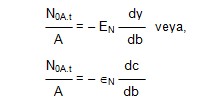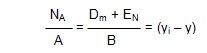Kütle Transferi; Difüzyon (diffusion)

Difüzyon, fiziksel bir uyarımla bir bileşenin bir karışım içindeki hareketidir. En önemli parametre, difüzlenen bileşenin konsantrasyon değişikliğidir. Konsantrasyon dalgalanması bileşeni, bu farklılığı bozacak ve eşit konsantrasyona ulaşmasını sağlayacak yönde hareket etme eğilimine sokar. Dalgalanma bozulmaz ve sabit bir halde devam ederse, difüzlenen bileşen akımı sürekli olur. Örneğin, su akımı ile temasta bulunan bir tuz kristalinin, yüzeyi yakınında bir konsantrasyon dalgalanması doğar; tuz, yüzeye dik bir yönde sıvı tabakaları arasına difüzlenir. Yüzeyden tuz ayrılması, kristal tamamen çözününceye kadar devam eder.

Basınç veya sıcaklık dalgalanmaları da difüzyona yol açan parametrelerdir. Burada konsantrasyon dalgalanmasının neden olduğu difüzyon üzerinde durulacaktır.

Kütle Transferinde Difüzyonun Rolü

Tüm kütle-transferi işlemlerinde en az bir fazda, çoğu zaman her iki fazda birden difüzyon meydana gelir.

Gaz absorbsiyonunda madde önce gaz fazdan geçerek fazlar arasındaki arayüzeye ve arayüzeyden de sıvı faza difüzlenir.

Distilasyon işleminde, zenginleştirme bölgesinde düşük kaynayan bileşen sıvı fazdan geçerek arayüzeye difüzlenir ve arayüzeyden buhara geçer. Yüksek kaynayan bileşen ters yönde hareket eder; buhardan sıvıya geçer.

Katı ekstraksiyonunda madde, faz arasından geçerek sıvıya girer. Sıvı ekstraksiyonunda rafinat fazından gelen madde önce arayüzeye, oradan ekstrakt fazına difüzlenir.

Kristalizasyon işleminde, ana sıvıdan kristallere madde difüzyonu olur; madde katı yüzey üzerinde toplanır.

Nemlendirmede sıvı fazdan difüzyon yoktur, çünkü sıvı faz saftır ve herhangi bir konsantrasyon dalgalanması olmaz; fakat sıvı-gaz yüzeye (veya yüzeyden), oradan da gaz faza (veya gaz fazdan) buhar difüzyonu vardır.

Kurutmada, sıvı haldeki su, katının içinden yüzeyine difüzlenir, buharlaşır ve sonra buhar olarak gaza difüzlenir.

DİFÜZYON TEORİSİ

Burada difüzyonun nicel ilişkileri incelenmiş, ekipman içindeki belirli bir yerde ve fazlar arasındaki yüzeye göre dikey bir yöndeki difüzyon dikkate alınmıştır. Durgun hal varsayılmıştır ve herhangi bir noktadaki konsantrasyonun zamanla değişmediği öngörülmüştür.

Difüzyon ve Isı Transferinin Kıyaslanması

Isı akışı ve difüzyon arasında bir benzerlik vardır. Isı transferinde yürütücü kuvvet sıcaklık dalgalanması, difüzyonda ise konsantrasyon dalgalanmasıdır. İki durumda da akı, dalgalanmayla doğru orantılıdır. Ancak ısı bir madde değildir, bir enerji şeklidir; bu nedenle daha ileri bir benzerlik düşünülemez. Isı bir noktadan bir diğerine akarken arkasında bir boşluk bırakmadığı gibi, ulaştığı noktada bir yer işgal etmez. Isının hızı diye bir kavram yoktur. Oysa difüzyon maddenin fiziksel olarak akmasıdır ve belirli bir hızla gerçekleşir. Difüzlenen bileşik arkasında bir boşluk bırakır ve geldiği yerde bir hacim kaplar.

Madde akışı olan difüzyon, ısı transferinde bulunmayan üç yeni sorunu karşımıza çıkarır:

1. Tüm bileşenlerin bir faz içerisinde olduğu düşünülmelidir. İki bileşenli bir karışımda hem A hem de B bileşenleri göz önüne alınır. Difüzyonun yönünde tüm fazın net bir akışı söz konusu olabilir. Bu net akış her bir bileşen akımının cebirsel toplamına eşittir.

2. Eğer arayüzeye dik olan tüm fazın net akışı sıfırdan farklı ise fazın kütlesi yükselir veya düşer; arafazın kütlesi tüm fazların kütlesinin toplamını sabit tutmak üzere değişir.

3. Madde bir hareket içerinde olduğundan, akımlar ve hızlar, kalanın değişken haline göre görecelidir.

Eşmolal (Equimolal) Difüzyon; Hareketsiz Fazın Hacmi

Sabit duran bir gözlemciye göre tüm fazda net bir hareketin olmadığını halde, gözlemciye göre herhangi bir yönde net bir molal akış söz konusu değildir. Tüm A moleküllerinin kırmızıya ve tüm B moleküllerinin maviye boyandığını ve geçmeye başladıkça sayılabildiğini farz edelim. Kırmızı moleküllerin sağa ve mavi moleküllerin sola doğru hareketleri söz konusu olsun. Eğer gözlemci kırmızı moleküllere eşit sayıda mavi moleküllerin geçtiğini görüyorsa, bu durum moleküllerin net bir akışının olmadığını gösterir. Burada kütleler değil moller göz önüne alınmıştır. Net molal akışın sıfır olduğu durumda eğer kırmızı moleküller mavilerden daha ağırsa (yüksek molekül ağırlığı) net kütle akışı sağa doğru dur.

Moleküler Difüzyon; Fick Kanunu

Difüzyon olayı sadece moleküler hareketten doğar; ısı-transferi işlemindeki kondüksiyonla iletimde olduğu gibi. Difüzyon, moleküler ve türbülent hareketin birleşmesiyle olabilir; bu durum kondüksiyon-konveksiyonla ısı iletimine benzer. Sadece moleküler difüzyon olduğu, türbülent hareketin bulunmadığı durumda, A bileşeninin difüzyon hızı aşağıdaki denklemle verilir. Bu eşitliğe Fick Kanunu denir; ısı transferinde görülmüş olan Fourier Kanununun bir benzeridir.

D_mA = A bileşenin "molal difüzlenebilmesi"; N = molal akış hızı; N_0A / A = molal akı (ısı transfer akısı q/A ya benzer); dy_A/db = konsantrasyon dalgalanması (sıcaklık dalgalanması dT/db ye benzer); b = difüzyon yönünde faz sınırından olan uzaklık; A = kütle transferine dik yöndeki alandır.

B bileşeni için,

Moleküler difüzyon ısı transferi ile karşılaştırıldığında, N_0A/A ve N_0B/B nin molal akışları, ısı transferindeki akış q/A ya, difüzyon D_m termal iletkenlik k ya, ve konsantrasyon değişimleri dy_A/db ve dy_B/db, ısı değişimi dT/db ve benzerdir.

Tüm fazın kararlı olduğu iki-bileşenli bir sistem için,

Aynı molal difüzivite, iki bileşenli bir karışımın her iki bileşenine de uygulanabilir ve D_m her bir bileşen için de kullanılabilir.

Molal Difüzivite D_m (kg mol m^-1 s^-1)

Yayılma güçlerine kinetik gaz ve sıvı teorilerinde daha çok yer verilmiştir. Gazların bu özellikleriyle ilgili olarak yapılan çalışmalar, gazlar içindeki difüzyonun kinetik teorisinin daha iyi anlaşılmasını sağlamıştır.

Gazlar İçinde Difüzyon

Moleküler gaz difüzyonu moleküllerin lineer hareketinden kaynaklanırr. Herhangi bir anda gaz içindeki her bir molekül sıfırdan çok yüksek değerlere doğru değişen hızlarda rasgele yönlere hareket ederler. Verilen bir sıcaklık ve basınçta, ortalama hız sabit olup ~1000 ft/saniye kadardır. Bu kadar yüksek hızlar, konsantrasyonların moleküler difüzyonla hızlı bir şekilde eşitlendiği anlamına gelir. Geniş moleküler dağılımdan dolayı (1atm ve 32 ºF de yaklaşık 7.6x10²³ molekül/ft³) çarpışmalar o kadar sıklaşır ki, her molekülün yolu peşpeşe kesilir ve hızında çoğu zaman birim saniyede gerçekleşen büyüklük ve yön değişmeleri olur. Bu nedenle, 1atm ve 32 ºF da azot gazı moleküllerinin ortalama hızı 1490ft/saniye olmasına rağmen, her bir molekül her saniyede ortalama 5x10¹¹ kez gerçekleşen çarpışma yapar, ve konsantrasyon değişimi altındaki yığın hareketinin sonucunda etkili hızı küçük olur.

Küçük moleküller büyük moleküllere göre daha büyük ortalama hızlara ve düşük çarpışma sayılarına sahiptirler. Sıcaklık ne kadar yüksek olursa, ortalama hız o kadar büyük olur. Difüzyon sıcaklığın artmasıyla artar, molekül ağırlığı ve molekül boyutlarının artmasıyla azalır. Havada bulunan gazların difüziviteleri EK-17’de verilmiştir.

Difüzivetelerin Bulunması

Bir gaz içindeki difüzyon kinetik teoriden hassas bir şekilde tahmin edilebilir. Aşağıdaki uygulama yaklaşım metodunu göstermektedir. Aynı çap (d), ve kütlede (m) olan, n molekül içeren 1ft³ bir gazdaki moleküllerin ortalama lineer hızları aşağıdaki denklemle verilir:

u = ortalama doğrusal hız, ft/saniye; k =  Boltzmann sabiti, 5.65x10²⁴f t-lb_f/ºR; T = mutlak sıcaklık, ºR; m =  tek molekülün kütlesi, lb

Moleküller için ortalama serbest yol,

l = ortalama serbest yol, ft; d = molekül çapı, ft; n = her ft³ deki molekül sayısı

Şekil-1 de görüldüğü gibi bir gaz hacmi içerisinde AA gibi hayali düz bir düzlem olduğunu düşünelim. Gaz A ve B gibi iki bileşen içermektedir; düzlemde yer alan A nın mol kesri y dir. Moleküller düzleme her iki yüzünden yaklaşır ve içerisinden geçerek tüm yönlere doğru difüzlenir (yayılır).

Şekil-1: A taneciklerinin, birbirinden a uzaklığında bulunan düzlemlerde çarpıştıktan sanra a düzlemine moleküler taşınması

Eğer moleküller düzlemden ortalama serbest yoldan büyük olamayacak bir uzaklıkta hareketlerine başlarlarsa, düzleme dik olarak hareket eden moleküller diğer moleküllerle çarpışmadan varışlarını gerçekleştirir. Düzleme diğer yönlerden yaklaşan moleküllerin diğer moleküllerle çarpışmadan düzleme ulaşmalrı bekleniyorsa, bunlar, λ dan daha az dikey uzaklıklardan başlamak zorundadır. Ortalama olarak, AA düzlemiyle çarpışmadan düzleme ulaşacak moleküllerin orijin noktaları arasındaki uzaklık olan a, ⅔λ a eşittir. Orijinin bu uzaklığına uyan BB ve CC düzlemleri Şekil-1 de gösterilmektedir; bu yerlerde A nın mol kesirleri sırasıyla y_(-a) ve y_(+a) dır. Şekilde görüldüğü gibi, y nin 2a’ya kadar olan değişiminin sabit olduğu varsayılmaktadır.

BB düzleminden AA düzlemine doğru AA düzleminden yukarıya geçen moleküllerin sayısı duvar çarpışma sıklığı denilen Z_(-a) eşitliği ile verilir.

Burada Z_(-a) toplam AA düzleminin her ft² 'sinden birim saniyede yukarıya geçen moleküllerin sayısı olup, yukarı doğru akışı bildirir. Toplam akışın A molekülerinden oluşan kısmı,

Benzer şekilde AA düzleminden aşağıya doğru gelen, CC düzleminden geçen A moleküllerinin moleküler akışı,

AA düzleminden geçen A nın net moleküler akışı z_(-a) ve z_(+a) arasındaki farka eşittir. Birim saatteki lb mol cinsinden,

Burada N_a Avagadro sayısıdır (bir lb mol içindeki moleküllerin sayısı). Denklem (2) ve (3) deki yer değiştirmelerden,

BB ve CC düzlemleri arasındaki konsantrasyon değişimi lineer kabul edildiğindan, denklem aşağıdaki gibi verilir.

Denklem (5) y_(-a) – y_(+a) için çözülürken Denklem(4) ile gerekli yer değiştirmeler yapıldığında,

a = 2l/3 olduğundan,

Bu denklem,

Fick Kanunu eşitliğiyle kıyaslandığında,

Eğer A ve B bileşenlerinin molekülleri çap ve kütle olarak benzer ise, difüzyon, aşağıdaki moleküllerin ortalama lineer hız denklemleri,

dikkate alınarak çıkarılabilir:

İdeal gazlar için ρ_M = p/R₀T ve n = p/kT dir. D_m(AA) kısmi difüzyon katsayısıdır. A ve B molekülleri farklı çap ve kütlelere sahipse, difüzyon aşağıdaki denklemle verilir; d_AB= (d_A+ d_B)/2 dir.

Şekil-2: Difüzyonda çarpışma fonksiyonu

Denklem (6), normal şartlardaki difüzyonları hesaplamak için kullanılır. Özellikle yüksek sıcaklıklarda daha uygun veriler elde etmek için, A nın ve B nin bir molekülü arasındaki moleküller arası potansiyel etkileşimi göz önüne almak gereklidir. Chapman-Enskog kinetik teorisinden elde edilen en uygun denklem,

Burada T= mutlak sıcaklık, ºR; M_A, M_B = A ve B nin molekül ağırlıkları; r_AB = çarpışmadaki moleküler ayrılma, A⁰; r_AB = (r_A + r_B)/2; W = çarpışma fonksiyonu, kT/Є_AB nin bir fonksiyonu; Î_AB = moleküler etkileşim enerjisi, ft-lb_f ‘dir.

Çeşitli gazlar için çarpışma fonksiyonu Ω (Şekil-2) için r ve Є/k değerleri Tablo-1 de verilmiştir. Deneysel verilerin yokluğunda bu değerler, aşağıdaki denklemlerden hesaplanabilir.

T_c= kritik sıcaklık, ºR; T_b=normal kaynama noktası, ºR; V_c=kritik hacim, ft³/ lb mol

Sıvılarda Difüzyon

Sıvılar içindeki difüzyon teorisi, gaz difüzyonunda olduğu kadar ne yeterince geliştirilmiş ne de deneysel veriler yeterince uygundur. Sıvılar içindeki difüzivete, gazların içindekinden daha küçüktür. Sıvı difüzyonu, moleküler hızlardan ziyade moleküllerin birbirlerini çekme fonksiyonu olan ve sıvı içindeki molekülleri hareket ettirmek için gerekli olan enerjiye dayanır. Sıvılar içindeki difüzyon, konsantrasyonla yaklaşık olarak lineer değişme gösterir.

Sıvılar için difüzyon aşağıdaki eşitlikten hesaplanabilir.

D_m = difüzyon, lb mol/ft-saat; M_B = çözücünün molekül ağırlığı; T = mutlak sıcaklık, ºR;

ρ_M=çözeltinin molal yoğunluğu, lb mol/ft³; μ = çözeltinin viskozitesi, lb/ft-saat; V_A=normal kaynama noktasında çözünen sıvının molal hacmi, ft³/ lb mol; k₁ = çözücü için birleşme parametresi

k₁ su için 2.6, metanol için 1.9, etanol için 1.5, ve benzen, heptan, eter ve diğer bazı çözücüler için 1.0 dır. Denklem (8) elektrolitlere uygulanmaz ve sadece düşük konsantrasyonlarda geçerlidir.

Hacimsel Difüzivite, D_v

Gaz ve sıvı difüziviteleri için, Denklem (7) ve (8) yerine, yeterli ise deneysel veriler kullanılmalıdır. Bu tür veriler, fiziksel ve kimyasal verilerin standart tablolarında bulunabilir. Genellikle veriler, molal difüzivite D_m olarak değil, hacimsel difüzivite D_v olarak verilmektedir. Bu değerler D_m ye aşağıdaki denklemle ilişkilidir.

ρ_M karışımın molal yoğunluğudur. İdeal gazlar ve sıvılar için, ρ_M konsantrasyondan bağımsızdır, D_vA = D_vB. Eğer ρ_M ideal olmayan gazlar ve sıvılarda olduğu gibi konsantrasyonla değişirse, D_mA ve D_mB eşit olmaya devam ederken D_vA ve D_vB eşit olmazlar. Ayrıca, D_v basınçla ters olarak değişirken D_m basınçtan bağımsızdır).

Elde edilen D_v nin boyutları L² t^-1 dır. Tipik değerler  Ek 17 de verilmiştir. Termal difüzivite α, aynı boyutlara sahiptir. D_v için kullanılan genel literatür birimleri birim saniyede santimetre karedir. Birim saniyede santimetrekareyi birim saatte ft kareye çevirmek için, 3,600/30.48² = 3.875 ile çarpmak gerekir. Sıvılarda D_v değerleri genellikle seyreltik çözeltilere uygulanır.

ÖRNEK

10 atm ve 200 ºF daki florotriklorometan-azot sistemi için molal difüziviteyi D_m, lb mol/ft-saat ve volumetrik difüziviteyi (D_v) ft²/saat olarak hesaplayınız. (FCCl₃ ün kritik özellikleri: T_c = 388.4ºF, ρ_c = 3.44 lb/ft³, azot için, r_B = 3.681 A⁰, Î_B/k = 164.6 ºR; çarpışma fonksiyonu W  = 1.04)

Çözüm:

Çözümde aşağıdaki denklem kullanılacaktır.

T = 660 ºR, M_A = 137.5, M_B = 28, V_c = 137.5 / 3.44 = 4.00 ft³/lb mol, V_c = kritik hacim, r_B = 3.681  A⁰ (veriliyor)

Moleküler etkileşim enerjisi,

W  = 1.04. aşağıdaki denklemde yerine konur,

D_v yi bulmak için,

Hareket Halindeki Faz Yığınıyla (bulk) Difüzyon

Önceki paragraflarda, eşmolal olan birbirine zıt olan iki akım halindeki A ve B de olduğu gibi net bir akışın olmadığı şartlardaki difüzyonun oluşumundan bahsedilmişti. Çoğu difüzyon işlemlerinde difüzyon doğrultusu içinde tüm fazların net bir akışı vardır. Bu akış difüzyondan bağımsız olarak maddeyi bir yerden bir diğerine hareket ettirir. Bu şartlar altındaki yığın hareketi yönünde difüzlenen A bileşeni kendi difüzyon hızı yığınınkine eklendiğinden, sabit bir gözlemciye göre faz yığınından daha hızlı hareket ediyor gibi görünür. Zıt yönde difüzlenen B bileşeni ise yığından daha yavaş hareket ediyor veya duruyor gibi görünebilir.

Difüzyon Hızları

Akış ve hız arasındaki ilişkinin iki temede sentezlenmesi istenir: (1) durgun bir arayüze göre ve (2) bir bütün olarak faza göre. Şekil-3a’da görüldüğü gibi iki bileşenli akışkan bir faz içindeki bir bölümü düşünelim. MM, A ve bileşenlerinin difüzlendiği arayüzü temsil etsin. Arayüzün alanı A, ft² ‘dir. Hızların arayüze göre göreceli olduğunu varsayalıyor. Arayüzden faza geçen A ve B bileşenlerinin akımı sırasıyla N_A/A ve N_B/A lb.mol/ft²-saattir. Akışın durgun olmasından dolayı N_A/A ve N_B/A, arayüzeye paralel diğer düzlemlerden geçen akımlar olup arayüzeyden sabit bir uzaklığa sahiptir. MM den b ft uzaklıkta yer alan db kalınlığındaki bir dilim içerisindeki A ve B bileşenlerinin konsantrasyonları, c_A ve c_B lb,mol/ft³ dir. Difüzyon devam ettiğinden c_A ve c_B b ile değişim gösterir,  N_A/A ve N_B/A akımları sabittir.

Şekil-3a’da temel dilimin hacmi A db ft³ tür. Dilimdeki A bileşeninin miktarı Ac_A db lb mol’dür. Bu bileşenin akış hızı N_A mol/saat olduğundan dilimin içinden geçiş zamanı Ac_A db/N_A saat olur. Bu zaman içerisinde A akımı tarafından kat edilen mesafe db ft olduğundan arayüzeyden b uzaklıktaki A bileşeninin hızı,

Şekil-3: Tek faz boyunca akılar ve hızlar; (a) difüzyon yönleriyle paralel faz bölgesi, (b) hızlar arasındaki ilişkiyi gösteren vektör diyagramları; u_A = u_0A + u,  u_B = u_0BA + u

Bu durum, eğer tüm A molekülleri aynı hızda yığın hareketi yönünde hareket etseydi her A molekülünün durgun bir arayüzeye göre sahip olabileceği hız olarak da yorumlanabilir. Benzer şekilde, aynı yerdeki B bileşeninin hızı, u_B,

Tüm fazın akış hızı N_A + N_B mol/saat tir. Eğer fazın yoğunluğu ρ_M mol/ft³ ise, arayüzeyle ilgili tüm fazın hızı,

Tüm fazın hareketsiz olması durumunda, u = 0 ve N_A = – N_B dir. Tüm faz hareketsiz olsun ya da olmasın, bir bütün olarak faza göre A ve B bileşenlerinin hızları u_0A ve u_0B olarak gösterilmektedir. Bu bileşenlere uygun gelen akımlar N_0A/A ve N_0B/A ayrıca tüm faza görecelidir.

u_A, u_0A ve u hızları şu eşitliğe göre,

ve  u_B, u_0B ve u eşitliğine göre birbirleriyle ilişkilidir.

Bu ilişkiler Şekil-3b de vektör diyagramlarında gösterilmiştir. u_0A ve u_0B vektörlerinin farklı yönleri işaret ettiğine dikkat ediniz. Onların eşit büyüklükte olmaları gerekli görülmemekle birlikte Şekil-3’de ve Denklem (11 ve (12)’de de görüldüğü gibi bu durum sadece c_A=c_B olduğunda doğrudur.

u_0A, u_A ve u’nun Denklem (13) den,

Benzer şekilde, B bileşeni için Denklem (9), (10), (12) ve (14)’den,

c_A ve c_B konsantrasyonları şu denklemlere dikkat edilerek mol kesirlerine dönüştürülebilir.

burada ρ_M karışımın lb mol/ft³ cinsinden molal yoğunluğudur. Denklem (15) ve (16) c_A ve c_B için gerekli yer değiştirilmeler yapıldıktan sonra,

Bu denklemler transferin mekanizmasından bağımsızdır; hem laminer hem de türbülent akıma uygulanabilir.

Moleküler Difüzyon ve Laminer Akış için Birleştirilmiş Denklemler

Difüzyon sadece moleküler harekete dayandığı ve türbülans olmadığı durumda eğer D_m biliniyorsa, difüzyon denklemleri difüzyon hızını hesaplanmasını sağlamak için birleştirilebilir.

A bileşenin akış hızının N_A + N_B toplam fazına oranını veren z büyüklüğü,

Eğer D_m sabitse Denklem (19), fazın belirli bir kalınlığı için integre edilebilir. Konsantrasyon aralığının integrasyon B’ye uzaklığı küçük olduğu zaman, bu varsayım ikili karışımların tüm konsantrasyonlarında gerçekleşen gaz difüzyonu ve sıvı difüzyonu için doğrulanabilir. D_m ‘nin küçük değişiklikleri için D_m uç değerlerinin aritmetik ortalaması sabit olarak kullanılabilir. Difüzivite sıcaklıkla değişirken, sıcaklık sabit veya yaklaşık olarak sabit olmalıdır.

y = A bileşeninin, b = B olduğu yerdeki mol kesri; y_i = A bileşeninin, b = 0 olduğu yerdeki mol kesri

Denklem (20), arayüzeydeki N_A/A madde akışının, difüzivite (D_m) ile doğru orantılı ve kalınlık B ile ters orantılı olduğunu göstermekte olup, konsantrasyon değişimi veya konsantrasyon farkıyla ilişkili değildir. Bunun yerine arayüzeye veya yüzeyden tüm fazın sapmasıyla etkilenmektedir.

Denklem (20) iki bileşenli sistemler için geneldir ve bileşenlerin bireysel akımlarının herhangi bir kombinasyonunu açıklar. İki özel durum özellikle önemlidir.

Eşmolal (Eşitmolal) Difüzyon: Eşitmolal difüzyon içerisinde, destilasyon işlemlerinde sıklıkça rastlandığı üzere N_A + N_B sıfıra eşit olup N_A = - N_B. Böylece z’nin değeri, Denklem (18)’den, sonsuz olur ve Denklem (20) geçersiz hale gelir. Denklem(19) aşağıdaki bağıntıya göre kullanılır,

Ancak, z sonsuz olduğunda bu kesir bir birim olur. İntegrali alındıktan sonra Eştlik (19) aşağıdaki hale gelir.

Bu sonuç eşitmolal difüzyon için N_0A = N_A olduğuna dikkat edilerek Denklem (1) in direk integralinin alınmasıyla bulunmasıyla aynıdır.

Tekbileşen Difüzyonu: Gaz absorbsiyonu, süzme ve ekstraksiyonda, B bileşeni gibi rastgele seçilen bir bileşen arayüzeye göre hareketsizdir, ve sadece bileşen A arayüzeye veya arayüzeyden difüzlenir. N_B = 0 ve Denklem (18) den z = 1 dir. Denklem (20) aşağıdaki hale dönüşür

Eşmolal difüzyonu halinde A ve B bileşenlerinin konsantrasyon değişimleri Şekil 4a’da, tekbileşenli difüzyon için Şekil-4b’de görülmektedir.

Şekil-4: Eşmolal ve tekbileşen difüzyonunda konsantrasyon değişimi; (a) A ve B bileşenleri aynı molal hızlarda, ters yönlerde difüzlenirler, (b) A bileşeni difüzlenirken, B bileşeni arayüzeye göre hareketsizdir.

Her iki durumda da, A bileşeni için konsantrasyonlar arayüzeyde 0.9 ve dış sınırda 0.1 dir. Tekbileşenli difüzyonda N_B sıfır olmasına rağmen, B bileşeninin konsantrasyon değişimi sıfır değildir. Eğer tüm faz B bileşeninin sıvı tabakası boyunca arayüzeye doğru ya da arayüzeyden hareketini engellemek için gerekli hızda soldan sağa doğru hareket etseydi, arayüzeye göre hareketsiz olan bir gözlemci değişimleri görebilirdi. Bu durum yürüme bandı üzerinde ileriye doğru hareket eden birinin yürüme hızının geriye doğru olan hızla eşit olduğu durumla benzerdir. Bileşen B bir bütün olarak bir akım boyunca difüzlenir, fakat akımın kendisi aynı hızda zıt yönde hareket eder, ve bileşen B arayüzeye göre hareketsizdir. Şekil-4 de belirtilen durumlar arasında tüm fark göreceli hızların küçük miktarıdır.

Türbülent Difüzyon

Momentum ve ısı enerjisini taşıdıkları gibi hareket eden girdaplar bir türbülent akım içerisinde maddeyi bir yerden bir başka yere taşır. Türbülent akımların içindeki momentum ve ısı transferi için verilen Denklem (3-18) ve (12-47) nin benzerliğine dayanarak, kütle transferi için denklemler şöyle olur,

N_0A,t/A, A nın molal akımı olup bir bütün olarak faza göre türbülent akımdan dolayı oluşur, ve E_N ve Î_N girdap yayılma güçleridir. Tüm faza göre toplam molal akım aşağıdaki aşağıdaki şekilde yazılır.

Madde, arayüzeye göre tüm fazın yukarı doğru hareketi olsun veya olmasın, türbülent hareketle arayüzeye doğru veya diğer yönde transfer olabilir. Sonuç denklem,

Kütle Transferi Katsayıları

Arayüzeyi geçen akışın laminar olması durumunda kararlı haldeki moleküler difüzyona dayanan Denklem (20) D_m ve B ilinmesi durumunda kütle transfer hızlarının tahmin edilmesinde kullanılabilir. Bununla birlikte, uzaklık B akışın laminar olduğu durumlarda bile daima bilinmeyebilir. Bundan başka, eğer akım iyi tanımlanmış kanallardan geçiyorsa ve eğer akışkan sıkıştırılmış kulelerde ayırma ve uyanma oluşumlarının olmasına olduğu gibi katı şekillerle temas halinde geçiyor ise kritiğin üzerindeki Reynolds sayılarında genel tampon bölge ve türbülent merkez görünür. Elek tabakası ve sprey kolonlarında olduğu gibi spreyler veya kabarcıklardan ve onlara doğru olan transfer basit moleküler difüzyon mekanizmasından çok daha farklıdır. Bu gibi makinelerde kararlı bir hale varılacağı da şüphelidir. İlave bir komplikasyon ise A nın gerçek arayüzey alanının sıklıkla bilinmiyor olmasıdır. Sıkıştırılmış kulelerde, gerçek arayüzey alanı sıkıştırılmanın geometrik alanından daha az olduğu varsayılırken püskürtücüler ve kabarcıklarda bu alan bilinmemektedir. Prensipte, kütle transfer hızları Denklem (22) ile hesaplanabilirken gerçekte B ve E_N bilinmediği için bu doğru değildir. Kütle transferi aşağıdaki denklemte tanımlandığı gibi kütle transfer katsayılarının kullanılmasıyla ele alınmaktadır.

 k özel ısı transferi katsayısı h de olduğu gibi özel kütle transfer katsayısını belirtir, ve Ф tüm fazın arayüzeye yaklaşan veya uzaklaşan muhtemel hareketine neden olan göreceli bir hız faktörüdür. k Katsayısı aşağıda verilen denklemle yayılma güçleriyle ilişkilendirilir.

E_N bilinmeyen bir B uzaklığındaki ortalama girdap yayıma gücü olarak kabul edilebilir. Böylece k, tüm fazın hareketinden bağımsız moleküler ve türbülent difüzyon vasıtasıyla kütle transferine karı direncin bir ölçüsü olur. Bu gibi hareketler sonu oluşa transfer Ф faktörü aracılığıyla ayrıca dikkate alınır.

Denklem (23)'deki k nın tanımından y konsantrasyonu tüm fazın ortalama konsantrasyonudur ve eğer akıtmam olarak karıştırılmış ise ulaşılmaktadır. Bu durum, ısı transferinde h nin tanımlanmasında akımın ortalama sıcaklığının kullanılmasına benzerdir. Konsantrasyon böylelikle tanımlandığı zaman, onun madde dengesi içindeki kullanımıyla benzerlik gösterir.

k Katsayısı bir Drew-Colburn katsayısıdır. Diğer kütle transferi katsayıları kimya mühendisliği literatüründen bulunabilir, fakat sadelik için Denklem (23) te tanımlandığı gibi bu kitap boyunca genellikle k kullanılmıştır. V fazı için y ve L fazı için x altsimgeleri kullanılmaktadır. k nın birimleri lb mol/ft²saat (birim mol kesri). Sayısal olarak, bu Ф birim olduğu zaman birim mol kesrinin sürükleyici kuvveti altında 1 ft² alan içerisinden geçen birim saatteki mol içindeki A bileşeninin akış hızıdır.

Relatif Hız Faktör

Ф faktörü, aşağıdaki gibi bulunabilir.

Denklem (24)’deki k nın bu denklemde yerine konulmasıyla ve Ф eşitliği çıkarılır.

(z – y)_L,  z – y_i ve z – y nin logaritmik ortalamasıdır.

Eşmolal difüzyon için N_0A = N_A dır. Bir turbulent sistemdeki eşmolal difüzyon için Denklem(21) ün integrali alınır,

ve Denklem (24)’de yer değiştirmelerle,

Denklem (23) ile (26)’nin karşılaştırılması equimolal difüzyon için Ф = 1 olduğunu göstermiştir. Bu durum akış ister laminar ister türbülent olsun doğrudur.

Tekbileşenli difüzyonda z = 1 olup Denklem (25) aşağıdaki hali alır.

(y_B)_L, 1 - y ve 1 - y_i nin logaritmik ortalamasıdır. Burada göreceli hız faktörü inert veya hareketsiz bileşenin sınır konsantrasyonlarının logaritmik ortalamasıdır.

Sıvılarda Uygulanma

Denklem (23) ve (25) gazlara olduğu gibi prensipte sıvılara da uygulanır. Gazlardaki difüzyondan farklı olarak, sıvılardaki D_m konsantrasyonla değişir. Ayrıca, sıvılarda k ve D_m için deneysel veriler, genellikle göreceli hız faktörünü içeren bir yolla tayin edilir. Bunun yanında, D_m verileri seyreltik çözeltileri ikapsadığından, Ф yaklaşık olarak bir birimdir. Bu nedenlerden sıvılar için Ф=1 alındığında Denklem(23) genellikle sadeleşir; sıvı faz L fazı ise,

Difüzyonun Yönü

Yukarıdaki tartışmada, bileşen A nın arayüzeyden faza doğru difüzlendiği varsayılmıştır. Bu bileşenin arayüzeyden çok, arayüzeye doğru difüzlendiği daha uygundur. Aynı denklemler y_i-y veya x_i-x için y-y_i veya x-x_i yazılarak kullanılabilir.

Kütle Transferi Katsayılarının Deneysel Ölçümleri

Gerçek ekipmanlardaki kütle transferinin kompleksliğinden dolayı, gerçek ekipmanlarda kütle transferi için temel denklemler uygun değildir, ve uygun denklemler vermek için boyutsal analiz ve yarı teorik benzerliklerin ışığında basit metotlara güvenilmektedir. Probleme yaklaşım aşağıdaki adımlar takip edilerek yapılır:

1. k katsayısı fazlar arası etkileşim alanının bilindiği ve sınır tabakaları ayırımının olmadığı yerlerdeki deneysel araçlarda çalışılmıştır. Şekil-5 de gösterilen pratikte bazen kullanılan ıslak duvarlı kule bu tipin genellikle kullanılan aygıtıdır. Türbülent akıştaki akışkanlardan ve bu akışkanlara doğru olan kütle transferi hakkında değerli bilgiler verilmektedir. Islak duvarlı kule sıvı dikey tüpün üzerinden verilmektedir ve tüpün iç duvarı boyunca yerçekiminin etkisi altında aşağıya doğru akmaya neden olur ve tüpün içerisine gaz akışkanla temas halinde kule içerisinden geçerek akar. Genellikle gaz kulenin altından girer ve akışkanın akış yönüne ter olarak akar, fakat paralel akışta kullanılabilir. Islak duvarlı kule içinde, akış oluşumundaki bazı komplikasyonlar hariç arayüzey bilinmektedir ve çekim oluşumu mevcut değildir.

2. Etkileşim alanının bilindiği diğer deneylerde yapılmıştır. Yapılan işte kullanılan prensip, akan sıvı veya gaz akımının içindeki katı şekillerden maddenin çözülmesi veya buharlaşma hızının ölçülmesidir. Maddenin kendisinin katı kütlelerden çözülmesi veya buharlaştırılması ya da ıslak katılardan sıvıların buharlaştırılması kullanılmaktadır. Bu teknikte, alan bilinmektedir ve basit olarak buharlaşan ya da eriyen katının alanı olarak kabul edilmektedir. Katının kendisinin difüzyonundaki fazlar arasındaki arayüzeyde oluşan transfer edilen madde ile ilgili komplikasyonlar yok edilmektedir. Bu noktada bulunan veriler ıslak duvar deneylerindeki ilişkilerin sınır tabakaları ayırımının aktif olduğu durumlara uygulanması için kullanılabilir.

3. Son olarak, gerçek dolgulu kuleler, filtre tabakaları ve sprey araçları üzerine deneyler yapılmaktadır, ve 1. ve 2. paragrafta belirtilen deneylerden elde edilen sonuçların önerdiği hatlarla ilgili veriler bulunmuştur. Alan etkisi sadece k katsayısından ziyade ekipmanın birim hacmindeki transfer alanı olan a nın kullanılmasıyla elde edilen ka katsayısı ile hesaba katılmaktadır. Bulunan ilişkiler sadece k için değil ürün olan ka içindir. Faktör a nın bağımsız olarak geliştirilmesi için bazı ilerlemeler kaydedilmiştir, ve bu mümkün odlunda k katsayısı izole edilerek basit durumlar içinde kullanılabilecektir.

k ve ka'nın değerlerini bulmak için yapılan deneyler, N_A, A, y_i, y_γ niceliklerinin deneysel ölçülmesi, transfer şartlarına bağlı olarak Ф nın hesaplanması, Denklem(23) den k nın hesabı ya da cihazın tüm uzunluğundan ortalaması alındıktan sonra denginin bulunmasını içermektedir. Eğer A biliniyorsa ekipmanın toplam hacmi kullanılarak ka hesaplanabilir. Boyutsal analiz, deneyleri planlamak için kullanılmaktadır ve boyutsuz guruplarda ve denklemlerde oluşan sonuçlar yorumlanmaktadır. Sürtünme, ısı transferi ve kütle transferi arasındaki benzerlikler faydalı birer rehberdir.

Bu parçada, A alanının bilindiği hallerde sıvılar arasında veya sıvılarla katılar arsında oluşan kütle transfer için ilişkiler verilmektedir. Fazlar arsındaki alanın bilinmediği ekipmanlar için katsayılara sonraki bölümlerde değinilecektir.

Şekil-5: Islak-duvarlı kule

BİLİNEN ALANLARDA KÜTLE TRANSFER  KATSAYILARI

Boyutsal analiz

Kütle transferinin mekanizmasından k katsayısının difüzivite D_m ve akışın karakterini kontrol eden kütle hızı G, viskozite μ ve bazı lineer boyutlara D dayanması beklenmektedir. Arayüzeyin şeklinin süreci etkilemesi beklenebilir ki her şekil için farklı bir ilişki oluşmalıdır.

Transfer yüzeyinin herhangi bir şekli için,

Boyutsal analiz şu eşitliği verir:

Burada M tüm fazın ortalama molekül ağırlığıdır. Her ikisinin de molal nicelik olmasından dolayı tutarlılık için k ve D_m kullanılmaktadır. Denklem (27) Colburn’ün ısı transferine benzer. Nusselt’in ısı transferine benzeyen ikinci boyutsuz denklem, Denklem (27)’nin (DG/ μ) (μ/D_mM) ile çarpılmasıyla bulunur:

Gurup kD/D_m Sherwood sayısı olarak adlandırılmaktadır ve N_Sh olarak ifade edilir. Bu sayı ısı transferindeki Nusselt sayısına benzer. Gurup μ/D_mM Schmidt sayısı olarak anılır ve N_Sc ile gösterilir. Bu sayı Prandtl sayısına tekabül etmektedir. Schmidt sayı sıklıkla μ/ρD_v olarak yazılmakta olup buradaki ρ, lb/ft³ içindeki fazın yoğunluğudur. Tipik değerler Ek 17 de verilmiştir.

Gurup DG/m ise Reynolds sayısına karşılık gelir ve N_Re ile gösterilir.

Genel olarak j_M N_RE nin bir fonksiyonudur.

Islak Duvarlı Kuleler

Islak duvarlı kuleler için çeşitli ilişkiler mevcuttur (Şekil-5). Gillilan-Sherwood eşitliğin göre,

Bu denklem Reynolds sayısının 2000 den 35000’e kadar olan değerleri için, Schmidt sayısının 0.60 tan 2.5’ğa kadar olan değerleri için ve 0.1 den 3 atmosfere kadar olan basınçlarda uygulanabilir.

Islak duvarlı kuleler için J_M, şöyle yazılabilir:

Burada f pürüzsüz düzgünlükteki borulardaki akış için Fanning sürtünme faktörüdür. Bu ilişki ıslak duvarlı kulelerdeki düzeltme ve absorpsiyon için yeterince tatmin edicidir. Bu denklemte görülen benzerlik aynı ekipmandaki ısı ve kütle transferi için geneldir. Bir yanda ısı ve kütle transferi arasındaki benzerlik diğer yanda sürtünme kuvvetinin benzerliği yalnızca kabuk sürtünmesi için geçerlidir. Eğer akımın ayrılmasından bir sürüklenme mevcutsa toplam sürtünme için uygulanmaz.

Tekli Silindirlere Dik Akış

Şekil-6 da tekli silindirlere dik akış için j_M in N_Re ile olan ilişkisi gösterilmektedir. Çizgi ile gösterilen hat ısı transfer faktörü j_H noktalarını verir. Bu hat, bu sistem için ısı ve kütle transferi arasındaki yakın ilişkiyi gösterir.

Tek Kürelerden Geçen Akış

Şekil-7 de N_SH ‘ye karşı N_RE N_SC^2/3 gösterilmiştir. Bu şekildeki hat N_RE N_SC^2/3 nin düşük değerleri için N_SH = 2.0 asimptotuna yaklaşır.

Şekil-6: Isı ve kütle transferi, akış tek silindirleri geçer

Şekil-7: Isı ve kütle transferi, akış tek küreleri geçer

Şekil-8: Isı ve kütle transferi, katı yataklar içinden akış

Tablo-2: Alan Uygunluk Faktörü, f

Dolgulu ve Akışkan Yataklarda Kütle Transferi

Çeşitli partikül türlerinin yatakları ve akışkanlar arasındaki kütle transferine ait veriler Şekil-8 deki eğride özetlenmiştir. Bu noktalarda j_M faktörü yatağın Î porozitesiyle çarpılır ve transfer için uygun alanı ölçen f faktörüne bölünür. Kürelerin yataklarında sabitlenmiş ya da akışkan için f=1000 olup diğer partiküllerin değerleri Tablo-2’de verilmektedir. Şekil-8 deki absis, içinde lineer boyutun tek bir A_v partikülünün toplam yüzey alanının karekökü olduğu özel bir Reynold sayısı N’_RE dır.

Şekil-8 de kesikli çizgi sabit yatak içindeki kürelerin yüzeyine olan ısı transferini gösterir. Kütle transferi ile ilgili veriler arasında bir uyum bulunmaktadır.

KÜTLE TRANSFERİNİN PENETRASYON TEORİSİ

Türbülent akımdan durgun bir yüzeye ısı transferinde ısı transferi hızını belirlemeye yarayan iki model vardır. Bunlardan ilki olan kararlı hal denge laminer tabakası teorisi, transferin sadece iletimle olduğu laminar hareket içinde sürtünmeli bir filmin varlığını öngörür. Diğer model akışkanın elementlerin türbülent merkezden durgun yüzeye doğru aktığını, orada kısa bir süre bekledikten sonra akışkan yığınındaki diğer elementlerle yer değiştirdiğin varsaymaktadır. Yer değiştirme zamanı mekanik elementin hareketi ile yönlenir ki hasarlı yüzey değiştiricide olduğu gibi zaman t_r bilinir ve ısı transfer katsayısı ile belirlenir. Türbülent akımda yerleşme zamanı bilinmez, ayrıca tüm akışkan elementler için bu değer aynı değildir. Bununla birlikte, eğer t_L yüzeydeki akışkan elementlerin etkili ortalama yerleşme zamanı olarak tanımlanırsa türbülent sıvıdan katı yüzeye ısı transferi eşitliği uygulanabilir.

Teori, arayüzeye olan kütle transferi sürecine de uygulanabilir. Buna göre akışkan elementler ve arayüzey arasındaki kütle transferinin tamamiyle moleküler difüzyonla olduğu varsayılır. Şartlar zamanla değiştiğinden akışkan element içerisindeki herhangi bir yerdeki konsantrasyon aşağıdaki eşitliğe göre değişkenlik gösterir; burada b arayüzeyden olan uzaklıktır.

Basitlik için, arayüzeyden veya arayüzeye doğru difüzyonun eş-molal olduğu varsayılır ve göreceli hız faktörü bir birimdir. Bu şartlar altında transfer akımı aşağıdaki denklemle verilir.

t_L akışkan elementlerin arayüzeyde kaldığı ortalama zamandır. Buradan, eş-molal difüzyon için bireysel kütle transfer katsayısı,

Yüzey-yenilenmesi modeli denk molal difüzyonla sınırlı değildir. Göreceli hız faktörü bir birimde farklı olduğu zaman kütle transfer katsayısı bu denklemle verilir; fakat transfer akım için denklem aşağıdaki hali alır.

t_L zamanı akışkan hızı, özellikleri ve sistem geometrisinin bir fonksiyonudur. Deneysel olarak tayin edilmelidir. Isı transferiyle bazı durumlarda yüzey yenilenme modelinin transfer sürecini film teorisinden daha gerçekçi olarak temsil ettikleri görülmüştür. Bu model özellikle transfer yüzeyinin kazınmış yüzey biriminde olduğu gibi dışarıdan veya sürekli bir faz içindeki kabarcıkların veya damlaların akışıyla yenilendiği ya da etkilendiği durumlar için yararlıdır.

EK 17. GAZLARIN HAVADAKİ DİFÜZİVİTELERİ
VE SCHMİDT SAYILARI

1 atm. ve 32 ⁰F da

	Difüzivite		NSc = m / r Dv NSc = m / M Dm
	Volumetrik, Dv, ft2/sa	Molal, Dm, lb.mol/ft.sa.103
asetik asit	0.413	1.15	1.24
aseton	0.32	0.89	1.60
amonyak	0.836	2.33	0.61
benzen	0.299	0.83	1.71
n-bütil alkol	0.273	0.76	1.88
karbon dioksit	0.535	1.49	0.96
karbon tetraklorür	0.24	0.67	2.13
klor	0.36	1.00	1.42
klorobenzen	0.24	0.67	2.13
etan 0.42	1.17	1.22
etil asetat	0.278	0.77	1.84
etil alkol	0.396	1.10	1.30
etil eter	0.302	0.84	1.70
hidrojen	2.37	6.60	0.22
metan	0.61	1.70	0.84
metil alkol	0.515	1.43	1.00
naftalin	0.199	0.55	2.57
azot	0.52	1.45	0.98
n-oktan	0.196	0.546	2.62
oksijen	0.690	1.92	0.74
fosgen	0.31	0.86	1.65
propan	0.34	0.95	1.51
sülfür dioksit	0.40	1.11	1.28
toluen	0.275	0.77	1.86
su buharı	0.853	2.38	0.60

GERİ (proje çalışmaları)