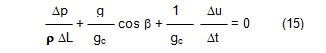Akışkanlar mekaniğindeki en önemli fiziksel ilkeler kütle
dengesi (veya devamlılık), mekanik enerji dengesi ve momentum dengesidir.
KÜTLE
DENGESİ
Kararlı akıştaki kütle dengesi basittir. akım sistemine
giren kütlenin hızı çıkan kütlenin hızına eşittir; çünkü kararlı koşullarda
kütle birikmesi veya azalması olmaz.
Akışkanın izlediği yol "akım hattı" terimiyle
tanımlanır. Bir akım hattı, akan bir kütlede hayali bir eğridir; eğri
üzerindeki her noktada net hız vektörü u, akım hattına teğettir. Böyle bir
hattı kesen net bir akış bulunmaz. Türbülent akışta girdaplar akım hattını
defalarca keserler, fakat bunların herhangi bir yöndeki net akışları sıfırdır.
Akım tüpü veya akım filamenti hayali bir borudur; duvarları
arasından akan kütlede net akış bulunmaz. Tüpün duvarlarına karşı akış olmadığından,
belirli bir zaman süresinde tüp içine akan akışkan kütlesinin hızı, tüpten
çıkan akışkan kütlesinin hızına eşit olmalıdır. Akım tüpü Şekil-10 da görüldüğü
gibi olsun. Akışkan, tüpün Sa kesitindeki yüzeyinden girsin ve Sb
kesitinden çıksın. Girişteki hız ve yoğunluk ua ve ra, çıkıştakiler ub ve rb dir. Akışkanın viskozitesinin
düşük (veya potansiyel) olduğu kabul ediliyor. Sa boyunca ua,
Sb boyunca da ub sabittir. Birim zamanda tüpe giren ve
çıkan akışkan aşağıdaki eşitlikle verilir.
Şekil-10:
Devamlılık
Ortalama
Hız
Akım tüpündeki akış potansiyel akış değil de, kayma
gerilimlerinin bulunduğu bir sınır tabakası içindeyse, Sa ve Sb
kesitindeki hızlar (ua ve ub) kesit içinde her noktada
farklı olur. Bu nedenle yerel ve ortalama hız kavramları bilinmelidir.
Bir akım tüpünün kesitinde diferensiyal bir alandaki kütle
akış hızı,
Kütle Hızı
Denklem(13) aşağıdaki gibi yazılabilir.
Akış kararlı (m = sabit) ve kesit değişmiyorsa (S = sabit),
G sıcaklık ve basınca bağlı değildir. Bu özellik daha çok sıkıştırılabilen
akışkanlar durumunda önemlidir; bunlarda V ve r, sıcaklık ve basınçla değişir. Kütle hızı G nin bir başka
tanımı da kütle akım yoğunluğu veya kütle akısıdır; akı, birim alandan birim
zamanda geçen herhangi bir miktardır.
ÖRNEK:
Ham petrol (öz ağırlığı, 60/60 0F da 0.887)
aşağıdaki şekilde görülen borudan akmaktadır. A borusu 2 in., B borusu 3 in. ve
C boruları 1.5 in.liktir (40 shc); C lerden eşit miktarda akım akmaktadır. A
daki akım 30 gal/dak (30 x 3.785 lt/dak.) dır.
(a) Her borudaki kütle akış hızının (lb/saat ve kg/sa),
(b) her borudaki ortalama dorusal hızın (ft/sn),
(c) her borudaki kütle hızının (lb/ft2.s) hesaplanması.
(a) Her borudaki kütle akış hızının (lb/saat ve kg/sa),
(b) her borudaki ortalama dorusal hızın (ft/sn),
(c) her borudaki kütle hızının (lb/ft2.s) hesaplanması.
Boruların boyutları ve kesitleri Ek-4 teki tablodan bulunur;
40 sch,
2 in. boru için kesit alanı =
0.0233 ft2
3 in. boru için kesit alanı =
0.0513 ft2
1.5 in. boru için kesit alanı =
0.01414 ft2 dir.
(1 ft = 30.48 cm, 1 lb = 0.454 kg, 1 g/cm3 =
62.37 lb/ft3,
1 ft3 = 7.48 gal = 28.316 l)
a. Her borudaki
kütle akış hızının hesaplanması.
Akışkanın yoğunluğu:
A ve B borularındaki kütle akış hızı yoğunluk x volumetrik akış hızına eşittir:
C borularından geçen kütle akış hızı, toplam akış hızının yarısına eşittir.
B boyunca olan hız, VB:
C boruları boyunca hız, VC:
c. Her borudaki
kütle hızı Denklem(14)ten hesaplanır.
A boyunca kütle hızı, GA:
B boyunca kütle hızı, GB:
C boruları boyunca kütle hızları, GC:
Paralel
Akışta Mekanik-Enerji Dengesi, Bernoulli Denklemi
Potansiyel akım halindeki bir akışkana Newton'un ikinci
hareket kanunu uygulandığında, sürtünme faktörü bulunmayan önemli bir denklem
elde edilir; bu eşitliğe Bernoulli denklemi denir, Denklem, sadece
mekanik-enerji terimlerinin bulunduğu özel bir enerji-dengesi denklemidir.
(Newton'un ikinci kanununu hatırlayalım: m = kütle, u =
doğrusal hız, F = maddeye etki eden tüm kuvvetlerin net sonucu olduğuna göre F µ
d (mu) / dt dir. mu = maddenin momentumudur. Newton hareket kanununa
göre bir maddeye etki eden net kuvvet, momentum hızının zamanla değişimi ile kantitatif
olarak ölçülebilir. Kütle sabitse F = kn m (du / dt) = kn
m a yazılır; a = du / dt = ivme, kn = orantı sabitidir. kn
= 1 / gc, gc = Newton kanunu dönüşüm faktörü denilen bir
sabittir ve sayısal değeri gc = 32.174 ft.lb/lbf.sn2
dir.)
Şekil-11: Akım
tüpü elementine etki eden kuvvetler
Bir akışkanın, kesit alanı sabit olan bir tüpten kararlı
potansiyel bir akımla aktığını düşünelim (Şekil-11). Akım tüpünün kesit alanı DS, akışkanın ortalama yoğunluğu r, tüpün sonundaki basınç ve hız,
p + Dp ve u + Du olsun
Tüp, eksene dik doğruyla b açısı yapacak bir konumda yerleştirilmiştir. Akım potansiyel rejimde olduğundan, akım tüpünün her kesitinde aynı hızda akar. Akımın geçtiği yol DL, bu yolu geçmek için harcanan zaman Dt dir. Akımın tümüne etki eden kuvvetler nelerdir? Tüpün silindirik bağlayıcı yüzeyine akım yönünde etki eden önemli bir kuvvet yoktur, çünkü bu yüzey üzerindeki basınç kuvvetleri akım yönüne diktir ve kayma kuvvetlerinin olmadığı kabul edilir. Akımı hızlandıran veya yavaşlatan kuvvetler,
- akım
yönündeki p DS kuvveti,
- akıma
zıt yöndeki (p + Dp) DS kuvveti,
- akıma
zıt yöndeki elementin ekseni yönündeki ağırlık kuvveti bileşendir.
Ağırlık kuvveti, elementeki akışkanın kütlesi ile ağırlık
ivmesi çarpımının gc sabitine bölünmesine eşittir.
Elementin kütlesi, ortalama yoğunluk r ile gösterildiğinde, r DS
DL, ağırlık kuvveti r DS
(g/gc) DL ve akım tüpü
ekseni boyunca bu kuvvetin bileşeni r
DS (g / gc) cos b DL
dir.
Buna göre akım yönündeki net kuvvet yazılabilir.
Bernoulli
Denkleminin Tartışması
Denklem(20), sıkıştırılamayan akışkanlar için önemli bir
eşitliktir. Buna göre, sürtünme olmayan bir akışta u hızı azaldığında, Z nin
üzerindeki yükseklik (DZ), veya basınç
(Dp), veya herikisi birden yükselir.
Yükseklik değiştirilirse, ya basınç veya hız değişir. Bernoulli denklemindeki
basınç, yükseklik, hız arasındaki birbirine dönüşebilme özelliği, bu terimlerin
aynı birimlerle tanımlanması halinde anlaşılablir; bu birim
(g / gc) Z, 1 lb akışkanın mekanik-potansiyel
enerjisini, (u2 / 2 gc), 1 lb akışkanın mekanik-kinetik
enerjisini; (p / r), akışkanı tüp içine
iten kuvvetler tarafından yapılan mekanik işi veya tüpten çıkan akışkandan
alınan işi tanımlar. bu nedenlerle Denklem(20), enerjinin korunumu ilkesinin
özel bir yorumudur.
Bernoulli denkleminin uygulama alanı çok geniştir. Denklem,
Şekil-11 le açıklanan koşullardaki bir akım hattına (akışkanın 1 hacim birimi
ele alınmıştır) uygulandığı gibi, potansiyel akış halindeki bir akım tüpünde
herhangi bir kesitteki hız sabit olduğundan, tüpün tümüne de uygulanır.
Denklemin çıkarılmasında akım tüpünün doğrusal ve kesit alanının sabit
olduğunun kabul edilmesine rağmen, enerjinin korunma ilkesi eşitliğin değişken
kesit alanlı eğri akım tüplerdeki potansiyel akışlara da uygulanmasını mümkün
kılar. Tüp eğri şeklindeyse, hızın yönü değişir ve Bernoulli denkleminde
vektöryel hız yerine skalar (veya bileşke) hız kullanılır. Bir başka konu da
bir kesit alanı içinde hız değişmelerinin bulunması ve sürtünmenin etkili
olması halidir; bu durumda eşitlik, düzeltme faktörleri kullanılarak sınır-tabakası
akışına uygun şekle getirilir.
Bernoulli denklemini özel problemlere uygularken, akım hattı
veya akım tüpünün çok iyi tanımlanması, üst ve alt akım noktalarının
belirlenmesi gerekir. a ve b noktaları basınç, hız ve yükseklik bilgilerinin en
iyi bilindiği yerler olarak tercih edilir.
ÖRNEK:
Öz ağırlığı 1.15 (60 0F / 60 0F) olan
tuz çözeltisi üstü açık bir tankın dibinden 2 in. lik (sch 40) standart bir
boruyla boşaltılmaktadır. Boşaltma borusunun ucu, tanktaki tuz çözeltisinin
yüzeyinden 15 ft aşağıdadır.
Tuz çözeltisinin yüzeyinde bir akım-hattı oluştuğu, boşaltma hattının merkezinden geçerek atık noktasına ulaştığı ve akım hattı boyunca sürtünme olmadığı kabul ediliyor.
Boşaltma borusundan çıktığı noktada (ve boru içinde) akımın hızı nedir? (g = 32.17 ft/sn = 981 cm/sn, 1 ft = 30.48 cm).
Tuz çözeltisinin yüzeyinde bir akım-hattı oluştuğu, boşaltma hattının merkezinden geçerek atık noktasına ulaştığı ve akım hattı boyunca sürtünme olmadığı kabul ediliyor.
Boşaltma borusundan çıktığı noktada (ve boru içinde) akımın hızı nedir? (g = 32.17 ft/sn = 981 cm/sn, 1 ft = 30.48 cm).
Denklem(20) yi uygulamak için, tuz çözeltisinin yüzeyi a noktası, boşaltma noktasında akım-hattının ucu b noktası olarak alınır. Bu iki noktadaki basınçlar atmosfer basıncına eşit olduğundan, pa = pb ve pa / r = pb / r dur. Çözeltinin yüzeyinde ua ihmal edilebilir düzeydedir ve ua2 / 2 gc atılır. Yükseklikler Zb = 0 ve Za = 15 ft tir. Bu bilgiler Bernoulli denkleminde yerine konur.
Bernoulli
Denkleminde Katı Sınırlar İçin Düzeltme
Mühendislikte karşılaşılan akışkan-akımı problemlerin çoğu,
katı sınırlar nedeniyle oluşan sınır tabakalarından kaynaklanır. Borular ve
diğer sistemlerden akan akışkanda tüm akım sınır-tabakası akımı şeklinde
olabilir.
Bernoulli eşitliğinin bu tip akımlara uygulanabilmesi için
iki düzeltmeye gereksinim vardır. Birincisi, yerel hız u’nun sınır
tabakasındaki konumla değişmesi dolayısıyla, kinetik-enerji teriminde bir
düzeltme yapılmasıdır. İkincisi daha önemlidir ve akışkanın sürtünmesiyle
ilgilidir; sürtünme sınır tabakası oluşumuyla ortaya çıkar.
Bu koşullara göre düzeltilen Bernoulli denklemi, akışkanın
akmasında pompa kullanıldığında yapılan iş de dahil edilerek daha geniş
kapsamlı bir hale getirilir.
a.
Akımın Kinetik Enerjisi
Denklem(19) daki u2 / 2 gc terimi,
tümü aynı u hızında akan bir pound akışkanın kinetik enerjisini gösterir. Hız
akım kesit alanında değiştiğinde kinetik enerji aşağıdaki gibi hesaplanır. ds
Kesit alanındaki elementi inceleyelim.
Buradaki kütle akış hızı r u dS dır. dS alanından akan herbir
pound akışkan u2 / 2 gc ft.lbf/lb kinetik enerji
taşır ve dS alanındaki enerji akış hızı,
Aynı hız dağılım bilgisi, Denklem(13) teki V yı
hesaplamak için de zorunludur.
Sürtünmeli Akış
Sürtünme, mekanik enerjinin ısıya dönüşmesiyle kendini
gösterir. Sürtünmeli akışta,
Sıkıştırılamayan akışkanlar için Bernoulli Denkleminde
(Denklem-20) sağ tarafa bir terim (hf) ilave edilir. Böylece,
kinetik enerji faktörleri aa
ve ab nin de katılmasıyla Denklem(20)
aşağıdaki şekli alır.
Sürtünme sınır tabakasında olur. Çünkü Laminer ve türbülent
akışlardaki hız dalgalanmalarını sürdüren kayma kuvvetleri iş yapar ve yapılan
iş, viskoz etkisiyle ısıya dönüştürülür. Ayrılmamış sınır tabakasında oluşan
sürtünmeye "duvar=kabuk (skin) sürtünmesi" denir. Sınır tabakaları
ayrılıp iz hali meydana geldiğinde ilave enerji kaybı olur, bu "şekil
(form) sürtünmesi" dir; katı sınırın konumuna ve şekline bağlıdır.
Şekil-8a daki hal tümüyle duvar sürtünmesi, 8b deki ise şekil sürtünmesidir
(duvar sürtünmesi önemsizdir). Denklem(24) deki hf, iki sürtünme
tipini de içerir.
c.
Bernoulli Eşitliğinde Pompa İşi
Akışkanın mekanik enerjisini artırarak akımı sürdürmek için pompa kullanılır. Denklem(24)le tanımlanan bir akım sisteminde a ve b noktaları arasına bir pompa konulsun. Pompaya verilen iş şaft işi Ws dir. Pompanın işi Wp,
 |
ÖRNEK:
Şekil-12 görülen sistemde öz ağırlığı 1.84 olan bir çözelti,
depo tankından bir pompayla 3 in. lik (Sch 40) çelik bir boruyla çekilmektedir.
Pompanın verimi %60, emme hattındaki hız 3 ft/sn dir. Pompa çıkışı 2 in.lik (40
sch) bir boruya bağlanmıştır ve çözelti, besleme tankı seviyesinden 50 ft
yükseğe basılmaktadır. Tüm boru sistemindeki sürtünme kayıpları 10 ft.lbf
/ lb dir.
Pompanın basıncı ne olmalıdır (pp – pb, lbf / in2) ?. Pompanın beygir gücü nedir (P, hp)?
Kesit alanları: 3 in boru için 0.0513 ft2, 2 in boru için 0.0233 ft2 dir. a =1 alınabilir. 1 g/cm3 = 62.37 lb/ft3, gc = 32.17 ft.lb/lbf.sn2.
Pompanın basıncı ne olmalıdır (pp – pb, lbf / in2) ?. Pompanın beygir gücü nedir (P, hp)?
Kesit alanları: 3 in boru için 0.0513 ft2, 2 in boru için 0.0233 ft2 dir. a =1 alınabilir. 1 g/cm3 = 62.37 lb/ft3, gc = 32.17 ft.lb/lbf.sn2.
Çözümde Denklem(26) kullanılır. Depo tankındaki sıvı
seviyesi a noktası, 2 inclik borunun boşaltma ucu b noktası olarak alınır. Her
iki noktadaki basınç atmosferik olduğundan, pa = pb dir.
a daki hız ihmal edilebilir, çünkü tankın çapı borunun çapına göre çok
büyüktür. Kinetik enerji faktörü a = 1
alınır (önemli bir hata olmaz). 1 ft = 0.3048 m, lb/in2 = 0.06084
atm = 0.07031 kg/cm2 dir.
fps (feet, pound, saniye) sistemi birimleriyle çözüm:
2 in.lik borudaki hız, Vb = ?
a. Pompanın
yarattığı basınç:
Denklem(26) pompa için yazılarak basınç hesaplanır; a=emme bağlantısındaki
nokta, b = boşaltma noktasıdır. Emme ve boşaltma arasındaki seviye farkı ihmal
edilir; bu durumda Za = Zb dir. Denklem(26) bu yoruma
göre aşağıdaki şekilde yazılır.
b. Pompanın kullandığı güç = P:
Wp ile kütle akış hızı çarpımının dönüşüm
faktörüne bölünmesiyle bulunur; dönüşüm faktörü, 1 hp = 550 ft lbf /
sn dir. Kütle akış hızı,
GERİ (proje çalışmaları)
