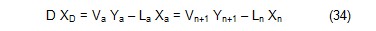Distilasyon işlemi iki yöntemle yapılabilir. Birincisinde
sıvı karışım kaynatılır, buhar haline dönüştürülür; buhar ayrılır ve
yoğunlaştırılır. İkinci yöntemde, kondensatın bir kısmı, oluşan buharla temas
edecek koşullarda geri döndürülür. İki yönteme de sürekli veya kesikli işlem
uygulanabilir.
BASİT
DİSTİLASYON
Basit distilasyon, çıkan buhar kalan sıvıyla dengede olacak
şekilde, sıvının belirli bir kesrini buharlaştırarak ayırmak ve
yoğunlaştırmaktır. Şekil-25 te basit bir distilasyon sisteminin kısımları
görülmektedir. Sıvı a pompasıyla b ısıtıcısına beslenir, c vanasından geçerken
basıncı düşürülür. Buhar ve sıvı karışımı d buhar ayırıcısına girer; burada
buhar ile sıvı kısımların ayrılabilmesi için yeterli bir süre bekletilir.
Ayrılan akımlar denge halindedir. Buhar e hattıyla, sıvı g hattıyla sistemi
terk eder.
Şekil-25: Basit bir distilasyon sisteminin şematik görünümü.
İkili
Karışımların Basit Distilasyonu
İki-bileşenli bir karışımdan 1 mol, Şekil-25 deki sisteme
beslensin. Karışımdaki uçucu bileşenin konsantrasyonu XF (F = feed),
buhar olarak çekilen kısmın molal kesri f dir; 1 – f = sıvı halde kalan
kısımdır. Buhar konsantrasyonu YD, sıvı XB ise,
ÖRNEK
%50 Mol benzen ve %50 mol toluen karışımı, P = 1 atm
basınçta basit distilasyonla ayrılmaktadır. (a) Ayırıcıdaki sıcaklığı, (b)
ayırıcıyı terk eden sıvının bileşimini, (c) ayırıcıyı terk eden buharın
bileşimini diyagramla gösterin (tüm değerler f nin fonksiyonudur).
Diyagramın çizilebilmesi için önce f nin birkaç değeri için,
eğimi veren - (1 - f) / f ifadesi hesaplanır. Bu değerler eğim olarak
kullanılarak Şekil-4’de görülen benzen-toluen sisteminin denge eğrisi üzerinde,
herbiri (XF, XF) noktasından geçen bir dizi doğru hat
çizilir. Bu hatlar (Şekil-26 da görülmektedir) denge eğrisini XB ve
YD değerlerinde keser; eğri üzerinden XB ve YD
değerleri okunur. Her buharlaşmanın karşılığı olan sıcaklık Şekil-3 teki
diyagramdan bulunur. Sonuçlar aşağıdaki tabloda toplanmıştır. Bu verilere göre
sorulan (a), (b), (c) eğrileri Şekil-27 de çizilmiştir. Eğriler, hemen hemen
düz birer doğru şeklindedir. %0 ve %100 buharlaşmadaki sınırlar, "kabarcıklaşma"
ve "çiğlenme" noktalarını gösterir.
Şekil-26: Örnek problemin grafiği
Şekil-27: Örnek problemin sonuçları
Entalpi-Konsantrasyon Yöntemi
İki-bileşenli
karışımların basit distilasyon problemleri, Şekil-11 ve Şekil-28 deki entalpi-
konsantrasyon diyagramlarından yararlanılarak çözülür. Şekil-28, Şekil-11 deki
diyagramın basitleştirilmiş halidir:
Bileşimi XF ve
entalpisi HF olan sıvı bir besleme, bir ısıtıcıya mF lb /
sa hızla aktığında, q Btu / sa ısı alır ve kısmen buharlaşır. Isıtıcıyı terk
ettikten sonra sıvı ve buhar adyabatik olarak birbirinden ayrılır. Sıvı ve
buhar akımlarının bileşimleri ve relatif akış hızları, birbirleriyle dengede
oldukları kabul edilerek saptanabilir.
Şekil-28: Sıvı beslemenin kısmen buharlaşması ve adyabatik olarak
ayrılması
ÖRNEK
Önceki problemi entalpi-konsantrasyon yöntemiyle çözün.
Benzen ve toluenin fiziksel bazı özellikleri aşağıda verilmiştir.
Önce 0 0C'a göre entalpi-konsantrasyon diyagramı
çizilir. Sıvı benzenin normal kaynama noktasındaki entalpisi (cal / g mol):
Hbenzen = (80 – 0) x
0.423 x 78.11 = 2643.2 cal / g mol
Htoluen = (110.6 – 0)
x 0.435 x 92.13 = 4432.5 cal / g mol
Bu noktalar HX diyagramında, X=1.0 ve X=0 da işaretlenir ve
düz bir doğru ile birleştirilir. Benzen-toluen gibi ideale çok yakın sistemler
için doygun sıvı hattına çok yaklaşan bir doğru elde edilir.
Hbenzen = 2643.2 cal
/ g mol , X = 1
Htoluen = 4432.5 cal
/ g mol , X = 0
Molal buharlaşma ısıları:
benzen: 94.14 x 78.11 = 7353.2
cal / g mol
toluen : 86.80 x 92.13 = 7996.9
cal / g mol
Buna göre doygun benzen ve toluen buharlarının entalpileri:
Hbenzen buharı =
2643.2 + 7353.2 = 9996.4 cal / g mol
Htoluen buharı =
4432.5 + 7996.9 = 12429.4 cal / g mol
Bu iki değer, X = 1 ve X = 0 da HX diyagramına konulur ve
noktalar birleştirilerek düz bir çizgi şeklindeki doygun-buhar hattı elde
edilir.
Hbenzen buharı =
9996.4 cal / g mol, X = 1
Htoluen buharı =
12429.4 cal / g mol, X = 0
Düğüm hatlarını çizmek için gerekli olan yardımcı hat,
benzen-toluen karışımının kaynama-noktası diyagramı denge verilerinden yararlanılarak
(Şekil-3 ün tablosu) çizilir. Böylece Şekil-29 da görülen HX diyagramı elde
edilir.
İstenilen bileşimi bulmak için, diyagram üzerinde X = XF
= 0.50 noktasından absis eksenine dik bir doğru çizilir ve bununla doygun-sıvı
hattının kesiştiği noktadan geçen düğüm hattı saptanır.
Şekil-29: Örnek problemin entalpi-konsantrasyon
diyagramı
Bu düğüm hattının iki ucu, sıvı ve buharın bileşimlerini
gösterir; sıvı buharlaşması olmadığı ve f = 0 olduğu hali tanımlar.
Entalpi-Konsantrasyon yöntemi, basit distilasyon
problemlerinin çözümünde XY diyagramına kıyasla daha az uygulanır. Avantajı
gerekli ısının kolayca bulunabilmesidir.
Çok
Bileşenli Karışımların Basit Distilasyonu
r bileşen içeren bir sistemin basit distilasyonunda, her
bileşen için madde dengesi,
ÖRNEK
%30 mol n-heksan, %45 mol n-heptan ve %25 mol n-oktan içeren bir karışıma atmosfer basıncında basit distilasyon uygulanmaktadır. Beslemenin 0.60 ı buharlaştığında, (a) ayırıcının sıcaklığı, (b) ayırıcıyı terk eden sıvı ve buharın bileşimleri nedir?
A = n-heksan, B = n-heptan, C = n-oktan olsun. Denklem(29)
ve Ek-19(b) kullanılarak sıcaklık ve XB (Σ XB = 1.0)
değerleri bulunabilir. Sıcaklık 210 0F (98.9 0C) olsun; basınç
14.69 lb / in2 (1 atm) için K değerleri:
KA = 2.18,
KB = 0.99, KC
= 0.46 Denklem(29) dan,
Bu durumda sonuçlar:
SÜREKLİ
DİSTİLASYON; ZENGİNLEŞTİRMELİ
Basit distilasyon, kaynama noktaları birbirinden oldukça farklı bileşenlerin bulunduğu karışımlara uygulanır. Uçuculukları yakın olan bileşenler bu yöntemle birbirinden ayrılamaz; bu durumda fraksiyonlu sürekli distilasyon kullanılır.
İdeal
Tepsilerde Zenginleştirme
Bir kolonda tek bir tepsiyi veya ideal tepsiler kaskadını
ele alalım. Tepsiler yukarıdan başlayarak numaralandığına göre, Şekil-30 da
görülen n inci tepsiyi inceleyelim. Bunun hemen üstündeki (n-1) inci, altındaki
(n+1) inci tepsilerdir.
n Tepsisine iki akım girer ve iki akım çıkar. (n-1) den Ln-1
mol / sa hızla sıvı, (n+1) den Vn+1 mol / sa hızla buhar akımı gelir
ve n de birbiriyle etkileşirler. Vn mol / sa lık bir buhar akımı
(n-1) tepsisine yükselirken, Ln mol / sa lik bir sıvı akımı (n+1)
tepsine iner. Buhar akımları V fazında olduğundan konsantrasyonları Y ile, sıvı
akımları L fazında olduğundan X ile tanımlanır. Buna göre n inci tepsiye giren
ve çıkan akımların konsantrasyonları Şekil-30 da gösterilmiştir.
Distillenen karışımın kaynama noktası diyagramı Şekil-31 de
görülmektedir; Şekil-30 daki dört konsantrasyon bu eğriler üzerinde
işaretlenmiştir. İdeal tepsi tanımına göre, n inci tepsiyi terk eden buhar ve
sıvı dengededir; dolayısıyla Xn ve Yn denge
konsantrasyonlarını gösterir. Her iki fazdaki konsantrasyon kolonun yüksekliği
arttıkça artacağından, Xn-1 > Xn ve Yn >
Yn+1 dir.
Bu yorum Şekil-31 de görülmektedir. (n+1) tepsisinden gelen
buhar ve (n-1) tepsisinden gelen sıvı birbiriyle etkileştiğinde,
konsantrasyonları bir denge haline doğru kayar (Şekil-31 de okla gösterilen
yönlerde). Daha uçucu bileşenin (A) bir kısmı sıvıdan buharlaşırken, sıvı
konsantrasyonu (Xn-1) den Xn e düşer. Keza buhardan, daha
az uçucu bileşenin (B) bir kısmı yoğunlaşacağından, buhar konsantrasyonu Yn+1
den Yn e yükselir.
Sıvı akımlar kabarcıklaşma noktalarında ve buhar akımlar da
çiğlenme noktalarında bulunduklarından, A bileşenini buharlaştırmak için
gerekli ısı, B bileşeninin yoğunlaşmasıyla açığa çıkan ısıyla sağlanmak
zorundadır. Kaskadtaki herbir tepside A bileşeni buhar akımına, B sıvı akımına
transfer olur. Sıvı ve buhardaki konsantrasyon kolon yüksekliği ile arttığından
sıcaklık düşer; n tepsisinin sıcaklığı (n-1) den yüksek, (n+1) den düşüktür.
Zenginleştirme ve Sıyırma
Fraksiyonlu sürekli distilasyonda sistemde, besleme kazana
verilmektedir; kazandaki sıvıda zenginleştirme işlemi yapılmadığından saf bir
dip ürün alınamaz. Bu sınırlama beslenmenin, kolonun merkezi kısmından
yapılmasıyla önlenir. Böyle bir durumda sıvı besleme kolondan aşağı kazana
akar; bu tip kazan sistemine "geri-kaynatma (reboiler)" denir. Sıvı
akımı reboilerdan yükselen buharla zenginleştirme işlemine girer. Reboilera
ulaşan sıvının A bileşeni sıyrıldığından, dip ürün hemen hemen saf B
bileşenidir.
TEPSİLİ KOLONLARIN DİZAYNI VE ÇALIŞMA ÖZELLİKLERİ
Tepsili kolonların dizaynı ve çalışmasındaki önemli
faktörler, istenilen ayırmayı yapabilecek tepsi sayısı, kolon çapı, reboilera
giren ve kondenserden çıkan ısı, tepsiler arasındaki mesafe, tepsi tipinin
seçimi ve tepsilerin yerleştirmesindeki detaylardır. Genel ilkelere uygun
olarak, tepsili kolonların performans analizleri madde ve enerji dengelerine
dayanır.
İki-Bileşenli
Sistemler İçin Tüm Madde Dengeleri
Şekil-32 de, tipik bir sürekli distilasyon sisteminin madde
dengesi diyagramı görülmektedir. Kolona XF konsantrasyonunda F mol /
sa besleme yapılmakta, ve XD konsantrasyonunda D mol / sa tepe
ürünüyle XB konsantrasyonunda B mol / sa dip ürün alınmaktadır. İki
adet bağımsız tüm madde dengesi yazılabilir.
Toplam madde dengesi:
Şekil-32: Sürekli fraksiyonlama
kolonu için madde dengesi diyagramı
Net
akış Hızları
D değeri, kolona tepeden giren ve kolonun tepesinden çıkan
akımların akış hızları arasındaki farktır. Şekil-32 de kondenser dolayındaki
madde dengesi,
A bileşeni için benzer madde dengeleri yazılabilir.
Kolonun alt bölgesindeki net akış hızları da sabittir, fakat
yönleri aşağı doğrudur. Toplam maddenin net akış hızı B, A bileşenininki B XB
dir. Sıyırma bölgesinde genel bir tepsi, n yerine m alt indisle gösterildiğinde
aşağıdaki madde dengeleri yazılır.
Çalışma Hatları
Kolonda iki bölge olduğundan iki de çalışma hattı bulunur;
birisi zenginleşme, diğeri sıyırma bölgesi içindir.
a. Zenginleşme Bölgesi: Bu bölgede çalışma hattı Denklem(17)
ile verilmişti.
b. Sıyırma Bölgesi İçin: Besleme tepsisinin altındaki kolon bölgesinde Denklem(17) aşağıdaki şekilde yazılır.
FRAKSİYON KOLONLARININ ANALİZİ
Fraksiyon kolonları McCabe-Thiele yöntemi ve
entalpi-konsantrasyon yöntemiyle analiz edilebilir.
McCabe-Thiele
Yöntemi
Denklem(37) ve (38) ile tanımlanan çalışma hatları ve denge
eğrisi xy eksenine geçirildiğinde, basamak-basamak yapıdaki McCabe-Thiele
diyagramı elde edilir. Bu diyagram, zenginleştirme veya sıyırma bölgesinde,
belirli bir konsantrasyon farkını sağlamak için gerekli "ideal" tepsi
sayısını hesaplamada kullanılır. Denklem(37) ve (38) den görüldüğü gibi Ln
ve Lm sabit olmadıkça, çalışma hatları eğri şeklindedir ve sadece bu
refluks akımların konsantrasyonla değişimi biliniyorsa çizilebilir. Ancak, Ln
ve Lm, pek çok durumda önemli derecede değişmez ve sabit kabul
edilebilir.
McCabe-Thiele diyagramını çizmeden önce bazı kavramların
tanımlanması uygun olacaktır.
Sabit
Molal Taşkan:
Kolon besleme tepsisi dışında, herhangi bir tepsi n ile
gösterilirse,
Refluks
Oranı:
Fraksiyonlama kolonlarının analizinde "geri-akış
(refluks) oranı" denilen bir değer kullanılır; iki refluks oranı vardır:
biri tepe ürüne, diğeri buhara ait olan refluks oranlarıdır. Her iki oran da
zenginleştirme kolonundaki değerlerle tanımlanır.
Kondenser ve Tepe Tepsisi
Denklem(37), sabit molal taşkan için yazılır ve alt indisler
kaldırılırsa aşağıdaki şekli alır.
X = Y olduğunda,
Tepe tepsisi için McCabe-Thiele diyagramı, kondenserin
çalışma şekline bağlıdır. Şekil-33 te üst tepsi ve kondenserdeki madde
dengeleri gösterilmiştir. Y1 = üst tepsiden çıkan buharın, X1
= üst tepsiye gelen refluksın konsantrasyonlarıdır. Çalışma hattının genel
özelliklerine uygun olarak hattın üst ucu, (Xc, Y1)
noktasındadır.
Refluks ve sıvı ürünün elde edilmesi için en basit düzen,
Şekil-33(b) de görülen tek toplam kondenser sistemidir; kolondan gelen tüm
buharı yoğunlaştırır ve refluks ve ürünü verir.
Böyle bir sistem kullanıldığında üst tepsiden çıkan buharın,
üst tepsiye gelen refluksın ve tepe ürününün konsantrasyonları eşittir; XD
ile gösterilir. Çalışma hattının ucu, bu hattın diyagonali kestiği (XD,
XD) noktasıdır. Şekil-34(a) daki abc üçgeni üst tepsiyi gösterir.
Kısmı bir kondenser (veya tasfiye edici) kullanıldığında,
sıvı refluksın konsantrasyonu tepe ürünü ile aynı olmaz; Xc » XD.
Bazan seri bağlı iki kondenser kullanılır; biri kısmi (refluks için), diğeri
son (sıvı ürün için) kondenserdir.
Böyle bir düzen, Şekil-33(c) de görülmektedir. Kısmi
kondenseri terk eden buharın bileşimi Y' dir ve Y' = XD dir. Bu
koşullarda elde edilen diyagram Şekil-34(b) deki gibidir. Çalışma hattı,
diyagonal üstündeki (XD, XD) noktasından (a) geçer. Oysa
kolonun üst tepsisi a'b'c' üçgeni ile tanımlanır. Bir kısmi kondenseri terk
eden buhar, sıvı kondensat ile dengede olduğundan buharın bileşimi (Y') denge
eğrisinin ordinatıdır; apsis Xc dir. Kısmı kondenser (aba'),
distilasyon sisteminde ilave bir teorik basamağa eşdeğerdir.
Şekil-33: Üst tepsi ve kondenserler için
madde dengesi diyagramları
Şekil-34: Tepe tepsisinin grafikle
tanımlanması
Dip Tepsi ve
Reboiler:
Kolonun dibindeki davranış, tepesindekine benzer.
Denklem(38), sabit molal taşkan için yazılır ve X=Y eşitliği için
basitleştirilirse, X = XB bulunur.
Dip tepsi ve reboilerin madde dengesi Şekil-35 te
verilmiştir. Çalışma hattının ucu (Xb, Yr) noktasıdır; Xb
= dip tepsiden gelen sıvının, Yr = reboilerden gelen buharın
konsantrasyonlarıdır. Reboileri terk eden buhar sıvı dip ürünle dengededir;
denge eğrisi üzerindeki bir noktanın koordinatları (XB,Yr)
dir ve reboiler, ideal bir tepsi gibi çalışır. Şekil-36 da reboiler (cde) ve
dip tepsi (abc) için grafik tanımlar görülmektedir.
Besleme
Tepsisi:
Beslemenin debisinin artırılması, sıyırma kolonunda
refluksı, zenginleştirme kolonunda buharı veya her ikisini birden artırır.
Zenginleştirme kolonunda buhar akış hızı, sıvı akış hızından daha büyüktür.
Sıyırma kolonunda ise sıvı akış hızı, buhar akış hızından daha fazladır. Bunun
sonucu olarak, sıyırma kolonundaki çalışma hattının eğimi 1 den büyük,
zenginleştirme kolonundaki çalışma hattının eğimi 1 den küçüktür.
Besleme değişik koşullarda yapılabilir; soğuk sıvı, doygun
sıvı (kabarcıklaşma noktasında), sıvı ve buhar karışımı, doygun buhar (çiğlenme
noktasında), aşırı ısınmış buhar olabilir. Şekil-37 de farklı beslemeler
gösterilmiştir. Şekil-37a, soğuk sıvı haldeki beslemedir. Tüm besleme akımı,
sıyırma kolonunda refluksın bir kısmını oluşturur. Keza, beslemenin
kabarcıklaşma noktasına ısınmasıyla bir miktar buhar yoğunlaşır ve bu kondensat
L nin bir kısmını oluşturur. L, (1) zenginleştirme kolonundan
gelen refluks, (2) besleme, (3) kondensattan meydana gelir. Zenginleştirme
kolonuna giden buhar, sıyırma kolonundakinden yoğunlaşan kısım kadar daha
azdır. Şekil-37(b) deki besleme kabarcıklaşma noktasında bulunan sıvıyı gösterir.
Beslemeyi ısıtmak için yoğunlaşmaya gereksinim yoktur, dolayısıyla,
Bu beş değişik koşuldaki besleme tipi tek bir faktörle (f)
tarif edilebilir; f=giren herbir mol besleme için, zenginleştirme bölgesindeki
buhar akış miktarı (mol) dır. Değişik koşullardaki beslemeler için aşağıdaki
tanımlar yapılabilir:
Şekil-37: Değişik koşullardaki
beslemelerin, besleme tepsisinden akışı
Besleme
Hattı (q Doğrusu)
Denklem(44) ve (45), madde dengeleriyle beraber, tüm çalışma
hatları kesim noktalarının bulunduğu doğru denkleminin çıkarılmasında
kullanılır. Bu doğruya "besleme hattı (q doğrusu)" doğrusu denir ve
aşağıdaki eşitlikle tanımlanır.
Soğuk besleme için f sıfırdan küçük bir değer, kızgın (aşırı
ısınmış) buhar için birden büyük bir değerdir. Soğuk sıvı ve kızgın buhar için
f eşitlikleri aşağıda verilmiştir.
Soğuk sıvı:
Çalışma
Hatlarının Çizilmesi:
Çalışma hatlarını çizmenin en basit yöntemi:
(1) Besleme hattının yerleştirilmesi
(2) Y ekseni ile zenginleştirme hattının XD / (RD+1)
kesişme noktasının hesaplanması ve zenginleştirme hattının bu nokta ile (XD,
XD) noktasından geçirilmesi
(3) Sıyırma hattının, (XB, XB)
noktasından ve besleme hattıyla zenginleştirme hattının kesiştiği noktalardan
geçirilmesi
Bu yöntemlerle çizilen çalışma hatları Şekil-38 de
görülmektedir. XF. XB, XD, L, D sabit kabul
edilmiştir. Besleme soğuk bir sıvı ise besleme hattının eğimi yukarı ve sağa
doğru, doygun bir sıvı ise dikey, sıvı ve buhar karışımıysa yukarı ve sola
doğru, doygun buhar ise yatay, kızgın buhar ise aşağı ve sola doğru konumlardadır.
Şekil-38: Besleme doğrusuna besleme
koşullarının etkisi
Şekil-39: Besleme tepsisinin yeri
Besleme
Tepsisinin Yeri:
Çalışma hatları çizildikten sonra, Şekil-39 da görüldüğü
gibi, adım-adım çizilerek ideal tepsi sayısı bulunur. Çizime ya sıyırma
hattının altından (alt çalışma hattı) veya zenginleştirme hattının üstünden
(üst çalışma hattı) başlanır. Burada üstten başlandığı ve bir toplam kondenser
olduğu kabul edilmiştir. Çalışma hatlarının kesim noktaları birbirlerine
yakınlaşırken adımların, ne zaman üst çalışma hattından alt çalışma hattına
geçeceğine karar vermek gerekir. Bunun için her tepside azami zenginleşmenin
gerçekleşmesi ve tepsi sayısının mümkün olduğu kadar az olması istenir.
Bu ilke, X in değerinin, iki çalışma hattının kesiştiği
koordinattaki X değerinin altına düştüğü anda geçişin yapılmasıyla sağlanır.
Besleme tepsisi, daima bir üçgenle gösterilir; üçgenin bir
köşesi üst çalışma hattı, biri alt çalışma hattı üzerindedir. Optimum konumda
olduğunda üçgenin iki kenarı, çalışma hatlarının kesim noktasında birleşmiş
durumdadır; bu üçgen, besleme tepsisini gösterir.
Bir çalışma hattından diğerine geçiş, a ve b noktaları
arasında bulunan herhangi bir konumda olabilir, fakat besleme tepsisi optimum
noktadan başka bir yere konulduğunda gereğinden fazla tepsi sayısı çıkar.
Alt çalışma hattına geçiş b noktasına kadar
geciktirilebilir. Denge ve çalışma hatları arasındaki üçgenler gittikçe
küçülür; bunlar zenginleştirme bölgesinde gereksiz çok sayıda tepsiyi gösterir.
Benzer şekilde geçişin a noktasına yakın bir yerde yapılması durumunda, sıyırma
kolonunda gereksiz kolonlar bulunması sonucu doğar.
Isınma
ve Soğuma Gereksinimleri
Tepsiler adyabatik bir sistemdir ve dışarıdan ısı alış-veriş
olayı kondenser ve reboilerle ilgilidir. Molal gizli ısı l sabit ise, reboilere ilave edilen ısı qr
= V l, kondenserde
uzaklaştırılan ısı qc = – V l
dır. (Btu / sa veya cal / sa) (sisteme ısı verildiğinde ısı etkileri pozitif,
ısı alındığında negatif olur; dolayısıyla qc, negatiftir).
Isıtma ortamı doygun buhar
olduğunda, reboiler için gereken buhar,
Soğutma ortamı su olduğunda, kondenser içn gerekli su,
ÖRNEK
%40 Benzen ve %60 toluen içeren bir karışım, fraksiyonlu bir
kolonda sürekli distilasyonla ayrılacaktır. Karışım kolona 30 000 g / sa hızla
verilmektedir. Tepe ürününün %97 benzen, dip ürünün %98 toluen olması
istenmektedir (% ler ağırlıkçadır). Refluks oranı 3.5 mol / 1 mol ürün alınmıştır.
Benzen ve toluenin molal iç ısısı 7675 cal / g.mol, molekül ağırlıkları, Mbenzen
= 78, Mtoluen = 92 dir.
a. Tepeden ve dipten alınan ürünü, mol / sa olarak
hesaplayınız.
b. İdeal tepsi sayısını ve besleme tepsisinin konumunu
bulunuz: (1) besleme sıvı ise ve kaynama noktasındaysa; (2) besleme sıvı ise ve
20 0C de ise (öz ısısı = 0,44 Btu / lb 0F); (3) besleme 2
/ 3 buhar ve 1 / 3 sıvı ise.
c. Isıtma işleminde 20 lb / in2 basınçlı buhar
kullanıldığında, (1), (2), (3) halleri için saatte ne kadar buhar gerekir? (ısı
kayıpları olmadığı ve refluksin doygun sıvı olduğu kabul ediliyor.)
d. Soğutma suyu kondensere 80 0F da giriyor ve
150 0F da çıkıyorsa, saatte
kaç litre soğutma suyu gerekir?
a. Besleme, tepe ve dip ürünlerinin konsantrasyonları (benzenin
mol kesri cinsinden):
b. (1). Besleme sıvıdır ve kaynama noktası sıcaklığındadır.
İdeal tepsi sayısı =?, besleme tepsisinin konumu =?
Bunun için denge diyagramı çizilir. Diyagramda, XD,
XF, XB noktalarından çıkılan dik doğruların diyagonali
kestiği noktalar saptanır (Şekil-40).
Besleme hattının çizilmesi: f = 0 olduğundan X = XF
doğrusunun uzatılmasıyla besleme hattı çizilir. Çalışma hatlarının çizilmesi:
Denklem(42) den, zenginleştirme hattının y eksenindeki kesim noktası bulunur.
X = 0, Y = 0.216 koordinatları y eksenine yerleştirilir ve zenginleştirme hattı çizilir; bu hat ve besleme hattının kesiştiği nokta ile, X = 0.0235, Y = 0.0235 koordinatları birleştirilerek sıyırma hattı elde edilir.
Son aşamada iki çalışma hattı ve denge eğrisi arasında dik
açılı basamaklar çizilir. Elde edilen diyagramdan istenilen veriler okunur:
İdeal tepsi sayısı = 11 tepsi
besleme tepsisinin konumu = 7.
tepsi
b.(2) Besleme sıvıdır ve 20 0C sıcaklıktadır.
İdeal tepsi sayısı =?, besleme tepsisinin konumu = ? (beslemenin öz ısısı, cPL
= 0.44 Btu / lb. dir).
Çözüm b(1) dekine benzer; farkı besleme hattıdır. Şekil-3
teki kaynama noktası diyagramından beslemenin kabarcıklaşma noktası bulunur.
XF = 0.440 olduğundan, beslemenin kabarcıklanma
noktası = 95.3 0C
İdeal tepsi sayısı = 10 tepsi
besleme tepsisinin konumu = 5.
tepsi
b.(3). Besleme 2 / 3 buhar ve 1 / 3 sıvı karışımıdır. İdeal
tepsi sayısı =?, besleme tepsisinin konumu =?
Çözüm b(1) dekine benzer; farkı, besleme hattının eğimidir.
F = 2 / 3 olduğundan Denklem(46) dan besleme hattının eğimi bulunur.
İdeal tepsi sayısı = 12 tepsi
besleme tepsisinin konumu = 7. Tepsi
Şekil-42: Örnek problem, b(3)
c. Isıtmada kullanılan buharın basıncı 1.4 kg / cm2
dir. b(1), b(2), b(3) hallerinde gerekli buhar = ?
Zenginleştirme kolonundaki V buhar akış hızı,
Bu durumda gerekli ısı Denklem(49) dan hesaplanır.
d. Kondens suyun giriş sıcaklığı, 80 0F, çıkış sıcaklığı 150 0F; mC =? Llb / saattir?
Gerekli soğutma suyu miktarı, Denklem(50) den hesaplanır.
Kolon Verimi, Tepe Verimi
Endüstriyel uygulamalar açısından kolon tepsileri birer teorik denge kademesi değillerdir. Tepsilerde teorik dengenin kurulması uygulamadaki gaz veya sıvı akış hızlarında mümkün olmaz. Teorik dengenin oluşması ancak özel hallerde ve özel durumlarda mümkündür.
Distilasyon konusu incelenirken distilasyon kolonunun her
tepsisinde teorik dengeye ulaşıldığı varsayılmıştır. Oysa kolon toplam
veriminin (veya distilasyon verimi) hesaplanması istendiğinde, gerçek ve teorik
tepsi sayıları dikkate alınır.
Toplam verim E0 (efficiency), teorik tepsi sayısının,
gerçek tepsi sayısına oranı olarak tanımlanır:
Toplam tepsi verimini etkileyen çeşitli etkenler vardır; örneğin, akışkanın viskozitesi, buhar ve sıvı fazların akış hızları gibi hidrodinamikler ve kütle transfer özellikleri yanında, tepsilerin tipleri ve yapıları da önemli faktörlerdir. Asıl sorun, tüm etkenlerin dikkate alınarak toplam verimin nasıl hesaplanacağındadır.
Söz konusu verim (E0), sadece kolon içindeki tepsilerde
kaynaklanan verimdir. Sistemde bulunabilecek kısmi kondenser ve kısmi reboiler
de ayrı birer denge kademesi gibi çalışmalarına karşın toplam verim olarak
tanımlanan E0 kapsamında düşünülemez; böyle hallerde, diğer farklı
faktörlerin de dikkate alınması gerekir ki bu tür hesaplamalar çok karmaşık ve
güçtür. Bu nedenle, uygulamalarda genellikle tepsi veriminin kullanılması
tercih edilir.
Tepsi veriminin hesaplanmasında değişik yöntemler
kullanılır; Murphree, Walter ve Sherwood, Gillard, O’Connel, Geddes metotları,
gibi. Bunlardan en yaygın olarak kullanılanı Murphree metodudur.
Gerçek konsantrasyon noktalarını birleştirilmesiyle “sanal
(pseudo) denge” eğrisi oluşturulur. Mc.Cabe Thiele diyagramında tepsiler
sanal-denge eğrisi üzerinden oluşturulur. Bu durumda geçek tepsi sayısı, teorik
tepsi sayısına göre tepsi veriminin değerine bağlı olarak daha fazla bulunur.
Distilasyon kolonlarının zenginleştirici (rectifier) bölgesi
için EML eşitliğinin, sıyırıcı (stripper) bölgesi için de EMV eşitliğinin
kullanılması önerilir. EML ve EMV eşitlikleri kolondaki
n. ve n+1 nci tepsilere ait eşitliklerdir.
Şekil-43: Mc.Cabe Thiele diyagramı
Entalpi-Konsantrasyon
Yöntemi
Ponchon-Savarit yöntemi olarak tanıman analizde,
entalpi-konsantrasyon diyagramı kullanılır. Entalpi-konsantrasyon diyagramı iç
ısıları, karışma ısılarını ve hissedilir ısıları içerir. Diyagramda, aynı
zamanda, denge verileri de bulunur.
GERİ (proje çalışmaları)
