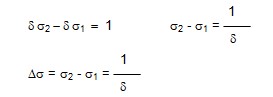Fransız matematikçisi Sean Fourier'in (1786-1830)
geliştirdiği ve Fourier transformasyon (dönüşüm) olarak adlandırılan bir
matematiksel işleme göre, bir dalga hareketi basit sinüs veya kosinüslü
ifadelerin toplamı ile tanımlanabilir.
y = A (sin 2 pnt + 1/3 sin 6 pnt + 1/3 sin 10 pnt
+..+ 1/n sin 2 npnt)
Üç sinüs dalgasından, genlikleri 5:3:1 ve frekansları 1:3:5
oranında olduğu halde, bu eşitlikle şekildeki kesiksiz grafik elde edilir. Bu
grafiğin kare dalga şekline çok yakın olduğu dikkat çekicidir.
Üç sinüs dalganın birleşerek bir
kare dalga şekline dönüşmesi
Fourier dönüşümü modern bilgisayarlar ile kolaylıkla
çözülebilen rutin işlemler haline getirilmiştir. Çoklu cihazların çoğunda
sinyal çözme işlemi "Fourier transform" a dayanır ve bu nedenle
Fourier transform cihazlar denir. Fourier transform aletleri sadece optik spektroskopiyle
sınırlandırılamaz. Nükleer magnetik resonans, kütle, ve mikrodalga
spektroskopileri ve ayrıca bazı elektroanalitik ölçmeler için de kullanılır.
Fourier transform spektroskopisini, ilk olarak 1950'li
yılların başında uzak yıldızların infrared spektra çalışmalarını yapan
astronotlar geliştirmişlerdir; bu kaynaklardan alınan çok zayıf sinyallerin
çevresel gürültülerden ayrılması sadece Fourier tekniği ile sağlanabilmektedir.
Fourier transform spektroskopinin ilk kimyasal uygulamaları, on yıl kadar sonra
uzak-infrared bölgede yapılabilmiştir. 1960'lı yılların sonunda uzak infrared
(10-400 cm-1) ve orta-infrared bölgelerde çalışabilen cihazlar
yapılmıştır.
Bir örneğin analiz prosesi aşağıdaki şekilde gösterilmiştir.
Siyah-cisim kaynaktan (1) çıkan infrared ışın demeti,
enerjiyi kontrol eden bir yarıktan geçerek spektral kodlamanın yapıldığı
interferometreye (2) girer. Oluşan interferogram sinyali örnek (3)
kompartımanına yönlendirilir; burada örneğin özelliğine ve analizin tipine göre
geçirilir veya yansıtılır. Enerjinin özel frekansları örnek tarafından
absorblanır. Örnek kompartımanından çıkan demet son ölçme için dedektörden (4)
geçer; dedektör, özel interferogram sinyalini algılayabilecek özellikte
olmalıdır. Ölçülen sinyal sayısallaştırılır ve bilgisayara (5) gönderilir;
burası Fourier transformasyonun gerçekleştirildiği kısımdır. Sonuç olarak IR
spektrum kaydedilir ve kullanıcıya sunulur.
Fourier Transform
Spektroskopinin Özel Avantajları
Örneğin, normal IR ve Fourier transform IR spektrofotometrelerde
m tane geçirgenlik ölçümünün yapılabildiği ve her bir pik noktanın (ki buna rezolusyon
elementler denir) birbirinden eşit frekans (veya dalga boyu) aralıklarında
bulunduğu bir spektrum düşünelim. Spektrumun kalitesi rezolusyon elementlerinin
sayısı çoğaldıkça veya ölçümler arasındaki frekans aralıkları küçüldükçe artar.
Bu nedenle spektral kaliteyi artırmak için m büyütülmelidir; rezolusyon
elementlerinin sayısı artırıldığında, spektrumun çizilme süresi de artar.
500-5000 cm-1 aralığını kapsayan bir infrared
spektra alınsın. Örnekte, 3 cm-1 aralıklarla pik veren rezolusyon
elementler bulunuyorsa her iki cihaz için harcanan zaman ve spektra kaliteleri
bu basit örnekle açıklanabilir. Normal IR için,
1500 x 0.5 = 750 saniye, veya 750 / 60 = 12.5 dakika
Rezolusyon elementlerin genişliği 3 cm-1 'den 1.5
cm-1 e düşürülürse daha yüksek spektral detay elde edilecektir; bu
durumda rezolusyon elementlerin sayısı da, ölçüm için gerekli zaman da iki kat
olacaktır.
Fourier transform için gerekli zamanın, normal bir
spektroskopide tek bir rezolusyon elementinin ölçülmesi için gerekli zamana
(0.5 saniye gibi) eşit olduğu kabul edilsin. 0.5 saniyede ölçülen bir Fourier
transformda 1500 rezolusyon elementinin herbirinin geçirgenlikleri birer defa
ölçülmüştür.
Normal spektropide ise aynı sürede bu elementlerden sadece
bir tanesinin geçirgenliği ölçülür, 1500 tanesi için 0.5 x 1500 = 12.5 dak.
harcanır. Oysa, 12.5 dak. süresinde 12.5 x 60/0.5 = 1500 tane Fourier transform
alınır, yani her bir rezolusyon elementinin geçirgenliği 1500 kere okunur;
değerler bigisayar kanallarında toplanır ve ortalamaları alınır.
Optik cihazların çoğunda, özellikle infrared bölgedeki
dizaynlarda rezolusyon elementinin genişliğinin azaltılmasıyla sinyal/gürültü
oranı da azalır. Bunun sebebi genişliği azaltmak için dar yarık kullanılması ve
dolayısıyla transdusere daha zayıf sinyallerin gitmesidir; infrared
dedektörlerde sinyalin azalmasıyla gürültüde bir azalma olmayacağından,
sinyal/gürültü oranı düşer.
Gürültülü bir ortamdan zayıf bir sinyali alabilmek için en
etkin yöntem sinyal ortalama yöntemidir. Bu yöntemde cihaza takılan bir sinyal
ayırıcı ile küçük sinyaller büyük gürültülerden ayrılır. Tekniğin uygulanabilmesi
için bir sinyalin tekrarlanabilir olması ve büyüklüğünün defalarca ölçülmesi
gerekir. Ölçmeler her seferinde birbirinin tam aynı şekilde yapılabilirse,
sonuçlar toplanabilir özelliktedir. Oysa gürültü düzensizdir ve birbirini
giderme eğilimindedir, n defa ölçme yapıldığında artışı n kadar değil sadece
kadardır. Bu durumda
sinyal/gürültü oranı da
faktörü kadar
iyileştirilmiş olur.
Yukarıdaki örnekte ölçme sayısı n = 1500 olduğundan, FTIR’de,
sinyal/ gürültü oranı (1500)1/2 kat veya yaklaşık 39 kat artırılmış
olur.
Cihazların çoğunda sinyal ortalama işlemi bilgisayarla
yapılır. Burada, ölçme işlemi çok sayıda tekrarlanır ve alınan sinyaller bir
veya daha çok kanalda toplanır. Yeterli sayıda tekrardan sonra sinyaller
toplanır ve ortalaması alınır.
Fourier transform tekniğinde olduğu gibi, tüm rezolusyon
elementlerinin aynı anda ölçümlerinin yapılabildiği spektroskopik yöntemlere
"katlı veya çoklu (multiplex) yöntemler" denir. Ultraviyole ve
görünür spektrada, sabit bir monokromatör ve bir Vidican tüpü ile yapılan
ölçmeler de katlı yöntemlerdendir.
Zaman-Bağımlı
Spektroskopi
Normal spektroskopiye frekans bağımlı spektroskopi denir,
bunda ışının gücü, ışının frekansına (saniye-1) veya dalga boyuna
göre kaydedilir.
Zaman-bağımlı spektroskopide ise, tersine, ışın gücünün
zamanla (saniye) değişimi incelenir.
Şekilde, (a) iki-ayrı frekanstaki ışının, (b) iki-ayrı
frekanstaki ışının birleştirilmiş halinin, ve (c) çok sayıda farklı frekanstaki
ışınların zaman-bağımlı ve frekans bağımlı spektrumları görülmektedir.
Şekil-a’daki eğri iki ayrı monokromatik kaynaktan gelen iki
ışının zaman bağımlı spektrumunu gösterir. n1
ve n2 frekansları,
aralarındaki küçük frekans farklılıklarının görülebilmesi için aynı grafiğe
alınmıştır. Burada güç P(t) zamanın fonksiyonu olarak çizilmiştir. Şekil-b'deki
eğri ise, iki frekansın da aynı kaynaktan gelmesi durumunda çizilen zaman bağılı
spektrumdur. İki dalga faza girerken ve çıkarken bir periyodiklik veya
"salınım" gösterir.
Kaynaktan çıkan ışında bir kaç dalga boyu olması durumunda
(şekil-c’de olduğu gibi), zaman bağımlı spektrum karmaşık bir hal alır. Dalga
boylarının sayısı arttıkça zaman skalasında bir tekrarı görmek zorlaşır. Bir
tekrar şeklin görülebilmesi için bazı dalga boylarının faza girip çıkması
gerekir. Çoğu kez birbirine yakın olan dalga boylarının faz dışına çok
çıkmalarıyla sinyal gücü zamanla zayıflar.
Zaman-bağımlı bir spektrum, frekans bağımlı bir spektrumla
aynı bilgileri içerir, bunlardan biri matematiksel işlemlerle bir diğerine
dönüştürülebilir.
Örneğin, Şekil (b), aşağıdaki eşitlikle Şekil (b1)'den
çıkarılmıştır.
P (t) = k (cos 2pn1t + cos 2pn2t + cos 2pn3t)
Burada k bir sabit, t zamandır. Hatlar arasındaki frekans
farkı, yaklaşık olarak %10 olayındadır.
Zaman ve frekans bağımlı spektrumların birbirine
dönüştürülmeleri, bir kaç hattan fazla frekans bulunması durumunda çok
karmaşıklaşır ve hesaplamalar çok zorlaşır, işlem ancak yüksek-hızlı
bilgisayarla yapılabilir.
Zaman Bağımlı Spektra
Çizme Yöntemleri
Zaman-bağımlı spektralarda, absorbsiyon spektroskopisinin
frekans aralığındaki ışın kullanılamaz (ultraviole için 105 Hz,
nükleer magnetik resonans için 107 Hz dır); çünkü algılama süresi
çok hızlı transduserler zaman-bağımlı spektralar için uygun değildir. Bunlarda
transduserin yüksek-frekanslı bir sinyalin sadece ortalama gücünü algılaması
fakat periyodik değişiklikleri görmemesi istenir. Bunun için de, yüksek-frekans
sinyali, sinyalle beraber taşınan zaman ilişkisini bozmadan, ölçülebilecek bir
frekansa değiştirilir (modülasyon); yeni oluşan sinyaldeki frekanslar orijinal
halindeki frekanslarla doğru orantılı olmalıdır. Spektrumun çeşitli dalga boyu
aralıklarında değişik sinyal değiştirme yöntemleri uygulanır. İnfrared bölgede
çoğunlukla Michelson interferometre yöntemi kullanılır.
Michelson Interferometreler
İnfrared ışını değiştirmede kullanılan aletler ilk defa
1891'de Michelsonun dizayn ettiği interferometreye benzer. Michelson
interferometre bir ışın demetini önce ikiye (yaklaşık eşit güçlerde) ayırır ve
bunların yarıları sonra tekrar birleştirilir; birleştirmeyi o şekilde yapar ki
birleştirilmiş demetin şiddetindeki değişiklikler, iki yarım demetin yolları
arasındaki farkın fonksiyonu olarak ölçülür. Şekilde infrared Fourier transform
spektroskopide kullanılan Michelson Interferometrenin şematik diyagramı
görülmektedir.
Bir Michelson interferometrenin
şematik diyagramı
Şekilde görüldüğü gibi, bir kaynaktan gelen ışın demeti paralelleştirilerek
bir ışın ayırıcıya gönderilir, burada ışının yarısı geçirilir diğer yarısı
yansıtılır. Böylece ikiye ayrılan demetlerden biri sabit diğeri hareketli bir
aynaya giderek yansıtılır; burada her bir demet yarısı örnek ve dedektör
yönünde, diğer yarısı kaynak yönünde gidecek şekilde tekrar ikiye bölünür; ilk
çıkan demetin sadece yarısı örnekten geçerek dedektöre ulaşır, diğer yarısı
kullanılmaz.
Hareketli aynanın yatay hareketi ile dedektöre giden ışın
dalgalanır. İki ayna da ayırıcıdan eşit uzaklıkta olduğu zaman, birleştirilmiş
ışını oluşturan parçalar tümüyle faz içindedir ve güç en yüksek düzeydedir.
Monokromatik bir kaynakta hareketli ayna, dalga boyunun tam 1/4 üne eşit
mesafelerde olacak şekilde her iki yöne doğru hareket eder, böylece yansıyan
demetin yolu da dalga boyunun 1/2 si kadar değişir (her bir yöne 1/4 dalga boyu
olduğundan). Bu koşullarda negatif (azaltıcı) girişim, birleştirilecek
ışınların gücünün sıfır olmasına neden olur. Daha uzak noktalara hareket, iki
yarım demetin tekrar faz içine girmesini sağlayarak tekrar pozitif (artırıcı)
girişimi oluşturur. İki ışının yolları arasındaki fark,
gecikme, d = 2(M - F)
Dedektör çıkışından alınan gücün gecikmeye göre çizilen
eğrisine de "interferogram" denir; monokromatik ışın için çizilen bir
interferogram yukarıdaki şeklin sağ tarafında görüldüğü gibidir ve bir kosinüs
eğrisine benzer (kosinüs eğrisi sinüs eğrisine tercih edilir, çünkü d = 0 olduğunda güç daima maksimumdur ve iki
yol uzunluğu birbirine eşittir).
Tipik bir infrared yazıcılı interferometrede ayna sabit bir
vM cm/sn hızla (bir motor ile) hareket eder. Pikler gelen ışının
dalga boyunun çok katlarındaki dalga boylarında olacağından, interferogramın
frekansı,
Aşağıdaki şekilde, sol kısımda zaman bağımlı interfeogramlar
ve sağ kısımda da bunların frekans bağımlı grafikleri görülmektedir.
İnterferogram ve optik spektraların
kıyaslanması
İnterferogramların Fourier Transformasyonu:
Şekil-a’da görülen interferogramın kosinüs dalgası teorik
olarak aşağıdaki eşitlikle tarif edilebilir:
P(d)
= B(s) cos 2 p f t
P(d)
= B(s) cos 2 p 2 vM s t
Ayna hızı, gecikme terimi ile veya aşağıdaki eşitlikle tarif
edilebilir.
P(d)
= B(s) cos 2 p d s
İki farklı frekans içeren bir interferogram için (Şekil-b),
P(d)
= B1(s) cos 2 p d s1 + B2(s) cos 2 p d
s2
Sürekli bir kaynak durumunda (Şekil-c) ise, interferogram,
sonsuz sayıdaki cosinüs terimlerinin toplamı olur.
Infrared Fourier tansform spektroskopi, p(d) yu d
nın fonksiyonu olarak çizer:
Uygulamada, sadece belirli gecikme aralıkları (birkaç
santimetre) için belirli büyüklükte örnek alma aralıklarındaki veriler
toplanabilir. Bu zorunluk, bir Fourier transform cihazının rezolusyonunu ve
frekans aralığını sınırlar.
Fourier Transform
Spekrometrenin Rezolusyonu
Bir Fourier transform spektrometrenin rezolusyonu, cihazın
tam olarak ayırabildiği iki bandın dalga sayıları arasındaki fark ile tarif
edilir. s1 ve s2 birbirinden ayrılabilen
infrared bandların dalga sayıları olduğuna göre,
Ds
= s2 - s1
İki bandın birbirinden ayrılabildiğini göstermek için, iki banda ait bir periyod veya tekrar eğrisini tam olarak veren zaman bağımlı spektrum çizilebilir. s1 ve s2 bandlarının rezolusyonları için, sıfır gecikmedeki bir maksimumundan, iki dalganın tekrar faz içinde olduğu ikici bir maksimumuna kadar interferogramının çizilmesi gerekir. ds2 nin ds1 den 1 kadar büyük olması durumunda da B deki maksimum oluşur.
Resolusyon ayna hareketinin uzunluğundan başka aynanın düz ve
ayırıcının eğikliğinden de etkilenir. Ayrıca interferometreye giren ışın
demetindeki ışınların birbirine yaklaşması veya uzaklaşması durumlarında da
resolusyon zayıflar.
İnterferogram Örneği
Bir interferogramın Fourier transformunu hesaplamak için,
eşit gecikme aralıklarında ışın gücü verileri alınır ve bilgisayarın
hafızasında biriktirilir. Rezolusyon elementlerin minimum sayısı (X) ile, bir
interferogramdan tüm detayları ile bir spektrum çizilebilir. X, aşağıdaki
eşitlikle bulunur.
Fourier Transform
Cihazları
Sürücü Mekanizma
İyi bir interferogram, hareketli aynanın hızı sabit olmalı
ve herhangi bir zamandaki konumu tam olarak bilinmelidir. Ayna düzlemi de, 10
cm'lik veya daha fazla aralıktaki tam bir süpürme işlemi boyunca sabit
kalmalıdır.
Dalga boylarının mikrometre seviyelerinde olduğu
uzak-infrared bölgede aynanın, bir dalga boyunun kesirleri için geldiği yeni
konum, motorlu bir mikrometrik vida ile tam doğru olarak ölçülebilir.
Orta- ve yakın-infrared bölgelerde ise daha hassas ölçme
yöntemlerine gereksinim vardır. Burada, ayna kasası paslanmaz çelik kollar
arasındaki hava yastıkları üzerinde tutulur. Kasa, bir mikrofondaki ses
sarımlarına benzer elektromagnetik bir sarım ile yürütülür; sarımdaki akımın az
bir miktarda artırılmasıyla ayna sabit bir hızda hareket eder. Ulaşması gereken
yere geldiğinde, akımın hızla ters yöne çevrilmesiyle süratle başlangıç
noktasına döner. Aynanın bir gidiş gelişi 2-18 cm arasında değişir; hareket
hızı 0.05-4 cm/sn aralığındadır.
Infrared bölgelerde başarılı çalışmalar yapılabilmesi için
ayna sisteminde iki önemli ilave özellik bulunmalıdır. Bunlardan biri hassas
gecikme aralıklarında interferogram örneklerinin alınması, ikincisi ise sinyal
ortalamasına izin veren sıfır gecikme noktasını tam doğru olarak saptayabilecek
yöntemin bulunmasıdır. Eğer sıfır gecikme noktası hassas olarak bilinemezse,
tekrarlanan süpürmelerden alınan sinyaller tümüyle faz içinde bulunmazlar ve
ortalama yöntemi ile sinyal artırılacağına (düzeltileceğine) daha da bozulur.
Hassas sinyaller alınması ve ortalama değerlerin bulunması
için modern cihazlarda bir yerine üç interferometre bulunur; bunlarda üç
hareketli ayna tek bir ayna kasasına yerleştirilmiştir. Her üç interferometre
sisteminin kısımları ve ışın yolları 1, 2 ve 3 alt kodları ile gösterilmiştir.
1 numaralı sistem küçük şekilde “örnek” eğrisine benzer bir
interferogram veren infrared sistemdir.
2 numaralı sistem çok bilinen "lazer-ışın, referans sistemidir",
bunda örnek alma-aralık bilgileri de elde edilebilir. Lazer sisteminde bir
helyum neon lazer kaynağı (S2), MM2ve M2
aynalarından oluşan bir interferometrik sistem, bir ışın ayırıcı (B2)
ve bir transduser (T2) bulunur. Sistem çıkışında sinüzoidal bir
sinyal elde edilir. Bu sinyal, elektronik olarak kare-dalgaya dönüştürülür;
birbirini takip eden sıfır geçişlerde örnek alma başlar veya biter. Lazer-ışını
referans sisteminde tekrarlanma yüzdesi çok yüksek, örnek alma aralıkları çok
düzenlidir. Pek çok cihazda, lazer sinyali aynı zamanda ayna-yürütme sistemi
hızını sabit seviyede tutma işlevini de yapar.
Üçüncü interferometre sistemine "beyaz-ışık"
sistemi denir ve tungsten bir kaynak (S3) ile görünür ışına hassas
bir transduser (T3) bulunur. Ayna sistemi sıfır gecikme verecek
şekilde yerleştirilmiş olup, analitik sinyaller algılama halinde sıfır noktasından
sola doğru hareket eder. Kaynak polikromatik olduğundan, sıfır gecikmedeki gücü
bu noktadan önce ve sonra oluşan herhangi bir sinyalden daha büyüktür. Böylece
bu maksimum, tekrarlanabilme dereceleri yüksek veri toplamada odak noktası
olarak alınır.
Modern fourier transform cihazlarındaki üçlü ayna dizaynı
frekansların çok hassas tayinine olanak verir. Böylece ulaşılan yüksek
tekrarlanabilirlik, ortalama işleminin çok sağlıklı yapılabilmesini sağlar.
Demet Ayırıcılar
Demet ayırıcılar, ışının yaklaşık %50'sini yansıtabilecek
seviyelerde refraktif indeksleri olan şeffaf malzemelerden yapılır.
Uzak-infrared bölgede çok kullanılan bir malzeme, refraktif indeksi düşük iki
katı madde arasına sıkıştırılmış ince bir Mylar filmidir. Orta-infrared bölgede
kullanılan ışın ayırıcılar sezyum iyodur (veya bromür), NaCl veya KBr üzerine
ince bir film halinde Ge veya Si çöktürülerek hazırlanır. Yakın-IR bölgede uygun
olan ayırıcılar CaF2 üzerinde demir (3) oksit filmi içerirler.
Kaynak ve Dedektörler
Fourier transform IR cihazların kaynakları, daha önce
anlatılan diğer infrared kaynaklara benzer. İlk çıkarılan cihazlarda, diğer IR
dedektörlere göre algılama zamanı daha kısa olan triglisin sülfat piroelektrik
dedektörler kullanılırdı. Şimdi ise hassasiyeti daha da fazla olan sıvı azotla
soğutulmuş civa/kadmiyum tellürür veya indiyum antimonür fotoiletken
dedektörler kullanılmaktadır. Başka tip dedektörler üzerinde de araştırmalar
sürdürülmektedir.
Fourier Transform Spektrometre
Tipleri
FTIR spektrofotometrelerde hız,
rezolusyon, hassasiyet ve doğruluk son derece yüksektir. Sistemde dispersiv
element bulunmaz (monokromatör yoktur). Michelson Interferometre ile tüm dalga boylarını
anında algılar, spektral bilgileri içeren girişim paternleri üretir.
Tek ve çift ışın yollu enstrüman
tipleri vardır. Uzak-infrared bölgede çalışan cihazlar çoğunlukla tek-ışın
yollu olarak dizayn edilirler. Daha yüksek frekans seviyelerindeki cihazların
çoğu çift-ışın yolludur.
Tek ışın yollu cihazlarda önce
referans, sonra örnek bilgileri kaydedilir; sonra örnekten referans verileri
çıkarılır. Çift ışın yollu cihazlarda doğrudan sonuç örnek spektrumu alınır.
Tek-ışın
demetli Fourier Transform IR Spektrometreler; FTIR
Çift-ışın
demetli Fourier Transform IR Spektrometreler; FTIR
Ticari Cihazların
Performans Özellikleri
Çeşitli frekans aralıklarında ve değişik ayırma gücüne sahip
Fourier transform spektrofotometreler vardır. Bazıları sadece uzak-IR bölgeyi
(~ 10 ile 500 cm-1) kapsayacak şekilde dizayn edilmişlerdir;
bunlardaki en iyi rezolusyon 0.1 cm-1 kadardır. Bazı cihazlar ise
orta-IR bölgede çalışırlar; bunların çoğunda kaynak ve demet ayırıcı, çeşitli
dalga sayıları aralığını elde edebilmek için değiştirilebilir özelliktedir.
Demet ayırıcılar, dedektörler ve kaynakların değiştirilebilir olması bir cihazın
görünür bölgeden uzak-infrared bölgeye (16000 cm-1 -10 cm-1
veya, 0.6-1000 mm) kadar
kullanılabilmesine olanak verir.
Cihazların rezolusyonları 2-0.06 cm-1 arasında
değişir. En yüksek rezolusyonda tam bir spektrumun alınması sadece birkaç
dakikada tamamlanır. Birkaç cm-1 kadar rezolusyonla çalışılması
halinde tüm spektrumun bir televizyon ekranına yansıtılması 1 saniyeden daha az
bir zamanda gerçekleşir.
FT IR Uygulamaları
Fourier transform spektroskopi, düşük ışın enerjisinin
önemli bir sorun olduğu hallerde başarılı spektrumlar alınmasını sağlar. Bu
cihazlarda verileri kazanma, dizme, sinyal ortalama, ve Fourier transformasyonu
kontrol eden çok gelişmiş bir bilgisayar bulunur. FTIR’ın dispersiv tekniğe
karşı önemli avantajları:
·
Hızlılık: Tüm
frekanslar aynı anda ölçüldüğünden FTIR ile yapılan ölçme işlemi sadece
saniyeler içinde tamamlanır. Bu özelliğe Felgett avantajı da denilmektedir.
İnterferometrik sistemin Fellgett avantajı, prizma veya gratingli cihazlardaki
sinyal/ gürültü oranlarını önemli derecede düzenler.
·
Hassasiyet: Hassasiyet
birkaç nedenle çok yüksektir. Kullanılan dedektörler daha hassastıt. İnterferometrenin
optik sistemi, dağıtıcı optik sistemlere kıyasla daha yüksek enerjili ışın
geçmesine olanak verirler (Jacquinot avantajı); bu durum gürültü seviyesinin
düşmesini sağlar, dedektöre ulaşan yüksek enerji hassasiyeti artırır.. Ayrıca,
hızlı tarama da sinyal/gürültü oranını yüksteceğinden, ilave bir gürültü
düzeltmesi elde edilir.
·
Mekanik Basitlik:
İnterferometredeki tek hareketli parça hareketli aynadır. Bu özellik sisteme
mekanik basitlik sağlar, parçalar takıp çıkarma işlemini en az düzeye düşürür.
·
iç Kalibrasyon: FTIR
enstrümanlarda, iç dalga boyu kalibrasyon standardı olarak HeNe lazerler kullanılır (Connes
avantajı). Sistemin kalibrasyonu kendi kendine yapılır, dışardan ir kalibrasyon
işlemine gerek olmaz.
Fourier transform cihazlarının tek
dezavantajı, cihazın ve bakımının çok pahalı olmasıdır.
Aşağıda, Fourier transform
spektroskopisinin önemli uygulamalarından bazı örnekler verilmiştir.
Uzak - İnfrared
Spektroskopi
Fourier transform yönteminin ilk uygulamaları, 400-10 cm-1
(25-1000 mm) aralığını kapsayan bölgede
yapılmıştır. İnterferometrik sistemin dağıtıcı sisteme kıyasla enerji yönünden
avantajlı oluşu daha kaliteli spektralar alınmasını sağlar. Ayrıca
spektrofotometrelerde, gratingde kırılan ışınların üst üste düşmesi nedeniyle
karmaşık bir durumla karşılaşılır.
Uzak-infrared bölge özellikle inorganik maddelerle çalışmaya
uygundur. Çünkü metal atomları ve inorganik (ve organik) ligandlar arasındaki
gerilme ve eğilme titreşimleri, çoğunlukla 600 cm-1 (>17 mm) den düşük dalga sayılarındaki frekanslarda
oluşur. Örneğin ağır-metal iyodürleri 100 cm-1 den düşük bölgede,
bromürler ve klorürler ise daha yüksek frekanslarda absorbsiyon yaparlar.
Metal-organik bağların absorbsiyon frekansları hem metal atomuna hem de
gruptaki organik kısmın karakterine bağlı olarak değişir.
İnorganik katı maddelerin uzak-infrared bölgedeki
çalışmalarından kristalin yapısı ve yarı iletken maddelerin geçiş enerjileri
hakkında önemli bilgiler de elde edilir.
Moleküllerin uzak-infrared bölgede absorbsiyon yapabilmeleri
için sadece hafif atomlardan oluşması ve ikiden daha fazla atomun (hidrojen
dışında) katıldığı iskelet eğilme titreşiminin bulunması gerekir. Buna örnek
olarak sübstitüe benzen türevleri gösterilebilir (bu bölgede birkaç absorbsiyon
piki vardır). Spektralar oldukça özeldir ve her bir maddenin tanımına olanak
verir; bu bölgede karekteristik grup frekansları da bulunur.
Uzak-infrared bölgede sabit dipol momenti olan gaz halindeki
moleküllerin saf dönme hareketlerinden oluşan absorbsiyonlar gözlenir. H2O,
O3, HCl ve AsH3 bu tip moleküllerdendir. Suyun
absorbsiyonu sıkıntılı durumlara neden olduğundan spektrometrenin sudan
temizlenmesi için uygun bir gaz geçirilir veya vakumla kurutulması gerekir
Orta - İnfrared
Spektroskopi
650-4000 cm-1 aralığını kapsayan bölgede Fourier
transform spektroskopinin uygulanmasıyla, bazı enerji sınırlamalarının neden
olduğu özel sorunlar en düşük düzeye iner. Örneğin, absorbsiyonun çok düşük
olduğu mikro miktarlardaki örneklerle çalışılabilir; 100 mm gibi küçük taneciklerin spektraları
alınabilir.Spektraların çok süratli alınmasını gerektiren kararsız maddeler
için de yöntem çok uygundur.
Tek-ışın yollu Fourier transform spektroskopi seyreltik
çözeltilerle çalışma da başarılı sonuçlar verir. Burada, solvent ve çözeltinin
interferogramları ayrı ayrı çekilir ve bilgisayarda toplanır. Saf maddenin
spektrumu, yine bilgisayarla verilerin birbirinden çıkarılmasıyla elde edilir.
Dağıtıcı-tip spektrometrelerde bu fark o kadar küçük olur ki bundan hareketle
maddenin tanımlanması yapılamaz. Fourier transform spektroskopinin sulu
çözeltilerle çalışmaya olanak vermesi önemli bir özelliğidir.
Gaz Kromatografik
Ayırmalardan Sonra Maddelerin Tanımlanması
İnfrared Fourier yöntemin orta-infrared bölgedeki en önemli
uygulaması, gaz kromatografik kolondan ayrılan fraksiyonların hemen,
"on-line" tanımının yapılabilmesidir. Bu tip bir analiz bir kaç
dakikada tamamlanmalıdır; böylece kaydedicili bir interferometrede olduğu gibi
süratle veri alınır. Bu uygulamanın detayları gaz kromatografi kısmında
verilmiştir.
Emisyon
Spektroskopisi
İnfrared ışını absorblayabilen moleküller, ısıtıldıkları
zaman infrared dalga boylarında ışın çıkarma (emisyon) özelliği de gösterirler.
bu olayın analitik uygulamalarda kullanılamayışının temel nedeni emisyon
sinyallerinin sinyal/gürültü oranının zayıf (küçük) olmasıdır, özellikle
örneğin sıcaklığı çevre sıcaklığına göre fazla yüksek değilse interferometrik
yöntemle son zamanlarda ilginç ve yararlı uygulamalar yapılabilmektedir.
İnfrared emisyon spektroskopi mikrogram seviyelerindeki
pestisaydların tanımlanmasında da kullanılabilir. Bu konuda yapılmış bir
çalışmada (I.Coleman and M.J.D low, spektrochim. Acta, 22, 1293, 1966) bir
Fourier transform spektrometreden yararlanılmıştır. Çalışmada pestisid örneği
uygun bir çözücüde çözülür ve bir NaCI veya KBr levhaya dökülerek çözeltisi
buharlaştırılır. Levha spektrometre girişine yakın bir yerde elektrikle
ısıtılarak kalan çözücü izleri de uzaklaştırılır. DDT, malatyon, ve dieldrin
gibi pestisidler bu yöntemle 1-10 mg a
kadar tanımlanabilirler.
İnterferometrik teknikle endüstri bacalarından çıkan
maddeler uzaktan izlenebilir.
Bu tip uygulamalardan biri, 8-inç yansıtıcılı bir teleskop
üzerine bir interferometre yerleştirilerek yapılır. Teleskop bacadan çıkan gaz
üzerine odaklanarak, CO ve SO2 bir kaç yüz feetlik uzaklıktan
algılanabilir.
