Katılarda Isı Akışı; Kondüksiyonla Isı Transferi (conduction heat transfer)

Kondüksiyonla iletim, homojen katılardaki ısı akışı ile incelenebilir; bu tip modellerde konveksiyonla ve radyasyonla ısı transferi yok gibidir. Konuyu anlayabilmek için önce "genel iletim kanununun, sonra katının sıcaklığının zaman içinde değişmediği "yatışkın (kararlı)-hal ısı iletim"in, ve sıcaklığın zamanla değiştiği bazı "yatışkın olmayan-hal iletimler"in öğrenilmesi gerekir.

Fourier Kanunu

Kondüksiyonla ısı akışının temel denklemi, izotermal bir yüzeyden geçen ısı akış hızı ve yüzeydeki sıcaklık dalgalanmaları arasındaki orantı ile verilir; A = izotermal yüzeyin alanı, q= yüzeye normal yöndeki ısı akış hızı, T = sıcaklık, n = ölçülen mesafe (yüzeye dik doğrultuda); k = orantı sabiti olduğuna göre,

Eşitlikteki kısmi türev, sıcaklığın hem konum ile ve hem de zamanla değiştiğini belirtir. Negatif işaret, ısı akışının sıcaktan soğuk tarafa doğru ve ısı dalgalanmasının ısı akışı ile zıt işaretli olduğunu gösterir.

A alanı ısı akışına dik bir yüzeydir; n ise A alanına dik doğrultuda ölçülen yolun uzunluğunu gösterir. Denklem(1), izotermal bir yüzeyden geçen ısı akışı için özel olmasına rağmen, herhangi bir yüzeyden geçen ısı akışı için de uygulanabilir. Bu durumda, A yüzeyin alanı, n de alana dik olan yol uzunluğudur. Fourier Kanununun bu şekilde genişletilmesi, ısının düz hatlar yerine eğriler boyunca aktığı iki- veya üç- boyutlu akımların incelenmesine olanak vermiştir. Bir-boyutlu akışta normallerle gösterilen ısı akış yönü doğrusaldır.  Bir-boyutlu ısı akışı, bir-boyutlu mayi akışına benzer ve geçilen yolu ölçmek için sadece bir doğrusal koordinat yeterlidir.

Bir-boyutlu ısı akışını Şekil-1 deki düz bir fırın duvarı örneğinde inceleyelim. Başlangıçta duvarın sıcaklığı, hava ile dengede olduğundan 25-26 ⁰C dir. Duvardaki sıcaklık dağılımı I çizgisi ile gösterilmiştir. Denge sıcaklığında T, zaman ve konuma bağlı değildir.

Duvarın bir tarafı 650 ⁰C deki fırın gazları ile aniden temas ettiğinde gaz ve duvar arasındaki ısı akışına karşı herhangi bir direnç olmadığı durumda, duvarın sıcak gazla temas eden tarafı kısa bir zaman içinde 650 ⁰C ye ısınır ve ısı akışı başlar. Bir süre sonra sıcaklık dağılımı, II ile gösterilen bir eğri boyunca ilerler ve C ile gösterilen bir noktanın sıcaklığı artar; bu durumda T, hem zamana ve hem de konuma bağlıdır. Bu prosese yatışkın olmayan-hal iletimi denir ve Denklem(1) şekildeki her noktaya her zaman diliminde uygulanabilir. Duvarın yeteri kadar uzun bir zaman sürecinde sıcak gaz ve soğuk hava ile temasta olması durumunda, sıcaklık dağılımı III çizgisiyle gösterilen şekli alır; bu dağılım zamanın uzamasıyla artık değişmez. Sabit sıcaklık dağılımındaki kondüksiyona yatışkın-hal kondüksiyonu veya iletimi denir. Yatışkın halde T sıcaklığı sadece konuma bağlıdır ve herhangi bir noktadaki ısı akış hızı sabittir. Yatışkın-hal bir-boyutlu akış için Denklem(1) aşağıdaki gibi yazılır.

Şekil-1: Fırın duvarlarının kararsız-hal ısınmasındaki sıcaklık dağılımları; duvarın, I. yüksek sıcaklıkla karşılaştığı ilk an, II. T zamanı süresince ısınması, III. yatışkın hale geldiği zaman

Isıl İletkenlik (Termal Kondüktivite)

Denklem(2) deki orantı sabiti k, maddenin fiziksel bir özelliğini tanımlar ve ısıl iletkenlik olarak bilinir.

Fourier Kanunu, k nın sıcaklık dalgalanmalarına bağlı olmadığını, fakat sıcaklığa bağlı olduğunu gösterir. Yapılan deneyler geniş bir sıcaklık dalgalanması aralığında k nın değişmediğini göstermiştir; ancak bu sonuç poröz (gözenekli) katıları kapsamaz. Poröz katılarda toplam ısı akışının önemli bir kısmını oluşturan tanecikler arasındaki radyasyon, doğrusal bir ısı kanununa uymaz, k sıcaklığa bağlıdır, fakat bu bağımlılık dar bir sıcaklık aralığında sabit kabul edilebilecek düzeydedir. Sıcaklık aralığı geniş ise, ısıl iletkenliğin T ile değişimi doğrusaldır.

a ve b deneysel sabitlerdir. Şekil-1 deki III doğrusu, k değeri sabit olan (b = 0 dır) bir katıyı gösterir; k sıcaklığa bağlı olduğunda bu doğru bir eğri şeklini alır.

Isıl iletkenlik değerleri maddeye göre değişir; metaller için en yüksek, toz maddeler için en düşük değerdedir. Gümüşün ısıl iletkenliği 3571 cal/cm.sa.⁰C (240 Btu/ft sa.⁰F) tır. k değeri düşük olan katılar izolasyonların yapımında kullanılır; bunlarda ısı akışının minimum olması istenir. Polistiren köpük gibi poröz izolasyon malzemeleri havayı hapsederek ısı konveksiyonunu önlerler. Bunların k değeri havanınkine yakındır. 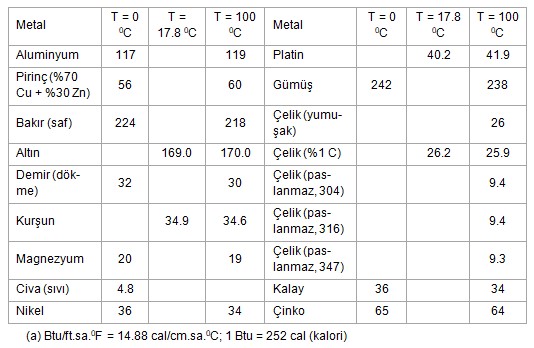Tablo-1 de bazı metallerin ısıl iletkenlikleri verilmiştir.

Tablo-1: Bazı Metallerin Isıl iletkenlikleri; 
k^(a), Btu/ft.sa.⁰F

YATIŞKIN – HAL ISI İLETİMİ

Yatışkın-hal ısı iletimi en basit olarak, Şekil-1 de görülen kalın bir duvar dilimi ile açıklanır, k nın sıcaklığa bağlı olmadığını ve duvar alanının kalınlığı ile kıyaslanamayacak kadar büyük olduğunu kabul edelim; bu durumda dilimin kenarlarından olan ısı kaybı ihmal edilebilir düzeydedir. Isı akışı duvara diktir.

Yatışkın-hal olduğundan, dilim içinde ısı toplanması veya azalması yoktur ve ısının akış yolu boyunca q sabittir. Sıcak taraftan olan mesafe x ile gösterilirse, Denklem(2) aşağıdaki şekilde yazılabilir.

Denklemdeki değişkenler x ve T olduğundan, doğrudan integrasyon,

x₂ – x₁ = B dilimin kalınlığı,dilimin iki tarafı arasındaki,

Isıl iletkenlik k sıcaklıkla doğrusal olarak değiştiğinde bile (Denklem-3), k yerine k A/B (ortalama) alınarak Denklem(5) uygulanabilir; ortalama değer, T₁ ve T₂ sıcaklıklarındaki iki yüzeyin k değerinin aritmetik ortalaması alınarak veya sıcaklıklarının aritmetik ortalaması ile k değerlerinden hesaplanarak bulunur. Denklem_(5), 1 ve 2 noktaları arasında katının ısıl direnci R ise aşağıdaki şekli alır (R = B / kA).

q hız, DT itici güçtür (yürütme kuvveti). Bir direncin tersi iletkenliktir; ısı iletiminde k = A/B dir. Direnç ve iletkenlik, k ya ve malzemenin boyutlarına bağlıdır.

ÖRNEK

Düz bir duvarın ısıl izolasyonu için 15 cm kalınlığında pulverize mantar kullanılmıştır. Mantarın soğuk tarafının sıcaklığı 4 ⁰C, sıcak tarafının 80°C, ısıl iletkenliği 0 ⁰C de 0.313, 93 ⁰C de 0.476 cal/cm.sa.⁰C dır. Duvarın alanı 2.32 m² olduğuna göre, duvardan ısı akış hızı kaç cal/sa tir? Bu değerin Btu/sa karşılığı nedir? (1 Btu = 252 cal)

Mantar tabakanın ortalama sıcaklığı T_ort = (80 + 4)/2 = 42 ⁰C dir; ısıl iletkenliğin 42 ⁰C deki değeri (k),

Seri Birleşik Direnç

Şekil-2 deki gibi A, B, C tabakalarından meydana gelen düz bir duyar düşünelim. Tabakaların kalınlığı, sırasıyla B_A; B_B; B_C; ortalama iletkenlikler k_A, k_B, k_C ve duvarın ısı transfer alanı A olsun; A, B, C tabakalarından ısı düşüşleri DT_A, DT_B, DT_C ile gösterilsin. Tabakalar birbiri ile tam bir ısıl temastadır ve yüzeyleri arasında sıcaklık farkı yoktur. Tüm duvar boyunca olan toplam sıcaklık düşüşü DT aşağıdaki ifade ile verilir.

Her tabakanın kendine özgü bir direnci vardır. Bunlardan akan ısı akış hızı ile, toplam sıcaklık farkı AT/duvarın toplam direnci olarak tarif edilen ısı akış hızının denklemlerini çıkaralım.

Şekil-2: Seri ısıl dirençler

Denkiem(5), k yerine, k kullanılarak her tabaka için ayrı ayrı yazılır.

ısı akışı kararlı olduğundan, birinci dirençten geçen miktar ikinci ve üçüncüden de değişmeden geçmelidir; q_A, q_B, q_C birbirine eşittir ve q ile gösterilebilir.

R_A, R_B, R_C tabakaların (A, B, C), R duvarın direncidir. Denklem(9) bir seri tabakadan akan ısıya karşı direncin, tabakaların dirençleri toplamına eşit olduğunu gösterir.

Bir iletkenden ısı akışı ile, kararlı elektrik akışı arasında yakın bir benzerlik vardır. Elektriğin akışındaki potansiyel faktör elektromotor kuvvettir ve akış hızı kulon/saniye veya amperdir.

Isının seri haldeki bir dizi dirençten akış hızı, elektrik dirençlerinden akan akıma benzer. Bir elektrik devresindeki dirençlerden herhangi birindeki potansiyel düşmesinin devredeki potansiyel düşmesine oranı, o direncin toplam dirence oranına eşittir. Aynı şekilde, ısıl bir devredeki potansiyel düşmelerinin (ki bunlar sıcaklık farklılıklarıdır) toplam sıcaklık düşmesine oranı, herbir ısıl direncin toplam ısıl dirence oranına eşittir. Bu yorum aşağıdaki matematiksel eşitliklerle gösterilir.

ÖRNEK

Düz bir fırın duvarı, ısıl iletkenliği 1.190 cal/cm.sa.⁰C olan 11.5 cm kalınlığında sil-o-cell tuğla tabakasıyla kaplanmıştır. Bu tabakanın üzerine, ısıl iletkenliği 11.90 cal/cm sa.⁰C olan normal tuğladan 23 cm lik bir tabaka kaplanmıştır. Duvarın iç yüzünün sıcaklığı 760 ⁰C, dış yüzü 77 ⁰C dir.

(a) Duvardan ısı kaybı kaç cal/sa tir? 
(b) Sil-o-cell tuğla ile normal tuğla arasındaki yüzeyin sıcaklığı kaç ⁰C dir? 
(c) İki tuğla arasındaki temas iyi değilse ve temas direnci 0.001 ⁰C.sa/cal ise, ısı kaybı ne kadardır? Duvarın alanı 930 cm² dir.

(a) Sil-o celi tabakanın (R_A) ve normal tuğla tabakanın (R_B) ısıl dirençleri,

Toplam direnç R,

Toplam sıcaklık düşmesi DT,

930 cm² duvardan ısı kaybı (Denklem-9 ile hesaplanır),

(b) Bir serideki dirençlerden birindeki sıcaklık düşmesinin bu dirence oranı, toplam sıcaklık düşmesinin toplam dirence oranına eşittir.

İki tuğla yüzeyi arasındaki sıcaklık farkı 760 – 568 = 192 ⁰C dir.

(c) Toplam direnç, bu koşullarda , temas direncini de içerir.

Isının Bir Silindirden Akışı

Şekil-3 teki gibi içi boş bir silindir düşünelim. Silindirin iç yarıçapı n dış yarıçapı ro ve uzunluğu L olsun. Silindirin yapıldığı malzemenin ısıl iletkenliği k dır. Dış yüzey T₀, iç yüzey T_i  sıcaklığındadır. Bu koşullar altında yarıçap doğrultusunda dışarıya ısı akış hızını hesaplayalım.

Şekil-3: Kalın duvarlı silindirden ısı akışı

Ana silindirin içinde yarı çapı r_i ve r₀ arasında bir r değerinde olan çok ince bir silindir bulunsun. Bu silindirin duvar kalınlığı dr dir; dr, d ye göre yeteri kadar küçükse ısı akışı çizgileri paralel kabul edilebilir ve Denklem(2) aşağıdaki şekilde yazılır.

Alan ısı akışına dik olduğundan 2 p r L ye eşittir ve Denklem(2)de dn = dr dir. Bu eşitliğin yeniden düzenlenip limitler arasında integrasyonu ile q ifadesi çıkarılır.

Denklem(12), kalın duvarlı bir silindirden akan ısıyı hesaplamakta kullanılır. Eşitlik, ısı akış hızı aşağıdaki şekilde ifade edildiğinde daha kullanışlı bir hale dönüşür.

Bu eşitlik, düz bir duvardan akan ısı için verilen Denklem(5) gibi genel bir denklemdir; farkı A_L terimidir. Eşitliğin doğru olması için A_l nin doğru saptanması gerekir. A_L terimi Denklem(12) ve (13) ün sağ tarafları birbirine eşitlenerek bulunur.

A_l, uzunluğu L ve yarı çapı r_L olan bir silindirin alanıdır, r_l,

Şekil-4: Logaritmik ve aritmetik ortalamalar arasındaki ilişki

Denklem(15)in sağ tarafındaki ifade kolayca hatırlanabilir, r_l ye logaritmik ortalama yarı çap denir. Logaritmik ortalama, aritmetik ortalamaya göre daha az kullanışlıdır, r₀/r_i = 1 olduğunda, aritmetik ortalama alınması önemli bir hataya yol açmaz. Logaritmik ortalama r_L nin, aritmetik ortalama r_a ya oranı r₀/r_i nin bir fonksiyonudur. Şekil-4 e göre r₀/r_i = 2 olduğunda, r_L = 0.96 r_a dır ve aritmetik ortalama kullanıldığında yapılan hata %4 tür; r₀/r_i = 1.4 olursa, hata %1 e düşer.

ÖRNEK

Dış çapı 6.4 cm olan bir tüpün üzerine, 5 cm kalınlığında asbestos(A) (k_A = 1.786 cal/cm.sa.⁰C) ve 4 cm kalınlığında mantar(B) (k_B = 0.446 cal/cm. sa.⁰C) tabaka kaplanmıştır. Tüpün dış yüzeyi 143 ⁰C ve mantarın dış yüzeyi 32 ⁰C olduğuna göre, ısı kaybı kaç cal/cm.sa tir? Tabakaların kalınlıkları fazla olduğundan logaritmik ortalama kullanılmalıdır.

Asbest tabaka için:

Mantar tabaka için: r₀ = 6.4/2 + 5 + 4 = 12.2 cm, r_i = 6.4/2 + 5 = 8.2 cm

Asbest A, mantar B ile gösterildiğine göre, dirençleri R_A, R_B dir.

YATIŞKIN OLMAYAN - HAL ISI İLETİMİ

Yatışkın olmayan-hal ısı iletimi geniş bir konu olup sadece bir-boyutlu iletim eşitliği incelenecektir. Yorumlarda k nın sıcaklığa bağlı olmadığı kabul ediliyor.

Şekil-5 teki gibi bir malzeme dilimi düşünelim. Dilimin sıcak tarafından x uzaklıkta dx kalınlığındaki ince bir dilim parçasını inceleyelim.

Şekil-5: Katı dilimde yatışkın olmayan-hal iletimi

Parçanın iki tarafı izotermal yüzeylerdir. Herhangi bir anda x te sıcaklık dalgalanması ¶T/¶x, dt zaman aralığında ısı girişi – k A (¶T / ¶x) dt dir; A dilimin alanı (ısı akışına dik), k ısıl iletkenliğidir. (x + dx) mesafesindeki sıcaklık dalgalanması, x dekinden daha büyüktür. Dilimin x mesafesinden ısı girişi ile, (x + dx) den olan ısı çıkışı arasındaki fark, dx tabakasında toplanan ısı miktarıdır ve, k A (¶²T / ¶x²) dx dt ye eşittir. Isı toplanması, dx in sıcaklığını yükseltir. Isı dengesi, öz ısı c_p ve yoğunluk r ile gösterildiğinde,

bulunur. Bu eşitlikteki a(cm²/sa) katının "ısıl difüzlenebilmesi (yayınırlık)" dir ve maddeye özgü bir özelliktir.

Yatışkın olmayan-hal iletim denklemi (Denklem-16), malzemenin biçimine göre farklı şekillerde çözülür. Her malzeme için yüzeyin sabit ortalama sıcaklığının (T_s), başlangıç sıcaklığının (T_a), tr zamanındaki ortalama sıcaklığının (T_b) ve Fourıer sayısının bilinmesi gerekir; Fourier sayısı malzemenin tabaka, küre veya silindir şeklinde oluşuna göre değişir. Denklem (16) nın çözümüyle elde edilen (T_s – T_b) /(T_s – T_a) değerlerinin, Fourier sayısına göre değişim eğrileri Şekil-6 da görülmektedir. Şekildeki ordinat (T_s – T_b) / (T_s – T_a), "tamamlanmamış sıcaklık değişikliğini gösterir.

Katılar bazan o şekilde ısıtılır ki, sıcaklık değişikliği katının sadece bir yüzeyi yakınında meydana gelir Böyle bir durumda Denklem(16)nın integrasyonu ile elde edilen,

eşitliği uygulanır. Burada Z = x / 2  (birimsiz), a = ısıl difüzlenme (cm²/sa), x = yüzeyden uzaklık (cm), t = yüzey sıcaklığındaki değişiklikten itibaren geçen zamandır(sa). Bu eşitlikteki (T_s-T) / (T_S-Ta) oranı Z = x / 2 ye karşı grafiğe alındığında, Şekil-7 deki eğri elde edilir. Eşitlik, yüzey sıcaklığı değiştikten sonra herhangi bir zamanda, katının tüm noktalarında sıcaklığın değiştiğini gösterir.

Şekil-6: Yatışkın olmayan hal ısınma veya soğuma sırasındaki ortalama sıcaklıklar; A: uzun bir dilim, B: bir silindir, C: bir küre malzemeye aittir. N_FO = Fourier sayısı, a = ısıl difüzlenebilme (cm²/sa, t_T = ısınma veya soğuma süresi (sa), s = dilim kalınlığının yarısı (cm), cm = yarı çap (cm)

Şekil-7: Bir katının kararsız hal ısınma veya soğuması

ÖRNEK

Sıcaklığı 21 ⁰C ve kalınlığı 2.54 cm olan düz bir plastik dilim 120 ⁰C deki iki levha arasına konuluyor, (a) Dilimin 99 ⁰C ortalama sıcaklığa gelmesi için ne kadar zamana gereksinim vardır? (b) Bu süre içinde plastiğin 1 cm² sine tansfer edilen ısı kaç kaloridir? Plastiğin yoğunluğu 0.899 g/cm³, ısıl iletkenliği 1.116 cal/cm.sa.⁰C, öz ısısı 0.40 cal/g.⁰C dir.

(a) Dilimin T_b = 99 °C ye gelmesi için gereken zaman t_T = ?

Şekil-6 dan sıcaklık farkı oranı 0.21 için, N_FO = 0.5 tir. Buna göre,

(b) 1 cm² plastiğe transfer edilen ısı, Q_T / A = ?

ÖRNEK

Ani bir soğuk dalgası atmosfer sıcaklığını 12 saat süreyle -23 ⁰C ye düşürmüştür, 
(a) Zemin başlangıçta 4.5 ⁰C ise, bir su borusunun donmaması için kaç cm derinliğe gömülmesi gerekir? (b) Bu koşullarda giricilik mesafesi ne kadardır? Toprağın ısıl difüzlemesi 11.15 cm²/sa tir.

(a) Yeryüzünün çok çabuk –23 ⁰C ye düştüğü ve bu sıcaklıkta kaldığı kabul edilsin. Su borusu 0 ⁰C iken donma tehlikesi yoktur.

T_s = - 23 ⁰C, T_a = 4.5 ⁰C, T = 0 ⁰C, T = 12 sa, a = 11.15 cm²/sa

Şekil-7 de, 0.84 değerinin karşılığı Z = 1.00 dir.

(b) Şekil-7 deki eğride (T_s –T) / (T_s – T_a) = 0.99 olduğunda, Z = 1.82 değerine ulaşmaktadır. Bu noktada x, x_p giricilik mesafesine eşittir, x = x_p. Buna göre,

GERİ (proje çalışmaları)