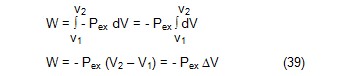Fizikokimyasal Sistemler; Temel Tarif ve Kavramlar (basic description and concepts)

Günlük yaşamdaki pek çok olay, temelde bilinmediği halde birtakım kurallar içinde gerçekleşir. Örneğin bir valizi kaldırmak için yer çekimine karşı bir dış kuvvetin uygulanması; masa üzerindeki bir kitabın enerjisinin, yere düşerken biçim değiştirmesi; her an çeşitli şekillerde karşılaşılan denge ve ısı olayları; ısınma, soğuma ve hava basıncı gibi doğa olayları; v.s., daima "Doğa Kanunları" denilen bazı kanunlar ve kurallar içinde gerçekleşir. Fen bilimciler bu kanunların çoğunu çözmüşler ve uzun deneyler ve çalışmalar sonunda matematiksel ifadelere dönüştürebilmişlerdir.

Kuvvet

Maddeye hareket veren kuvveti, Isaac Newton (1642-1727) aşağıdaki matematiksel ifadeyle tanımlamıştır.

Burada F bir madde parçacığına uygulanan "kuvvet"i, a parçacığın ivmesini gösterir; ivme, uygulanan kuvvetle aynı yönde vektöryel bir ifadedir. Eşitlikteki m orantı faktörüdür; buna kütle denir. İvme, hızın zamana göre birinci türevi, veya hız = yol / zaman olduğundan, yolun zamana göre ikinci türevidir.

Bu tarife göre Denklem(1) aşağıdaki şekilde de yazılabilir.

Buradaki kütle x hız'a "momentum" denir. Uluslararası Birim Sistemine (SI) göre kütle kilogram(kg), zaman saniye(sn), yol metre(m) ile verilir; bu durumda kuvvet birimi Newtondur (N). Newton çekim kanununa göre iki kütle arasında, bunların çarpımları ile doğru, aralarındaki uzaklığın karesi ile ters orantılı bir çekim kuvveti bulunur. G orantı sabitini gösterirse, çekim kuvveti F aşağıdaki eşitlikle verilir

Bir maddenin W ağırlığı, ona etki eden yer çekimi kuvvetidir; buradaki ivme g ile verilir ve vakumdaki serbest düşme ivmesidir. g, yeryüzünün çeşitli yerlerinde çok az farklılıklar gösterir.

Pratikte, bir maddenin kütlesi, ağırlığının bilinen standartlarla bir terazide kıyaslanmasıyla ölçülür (m₁ /m₂ = W₁ / W₂).

Mekanik İş

Bir F kuvvetinin uygulandığı nokta hareket ederse bu kuvvet "iş yapmıştır" denir. Uygulama noktası kuvvet yönünde dr kadar değiştiğinde, F kuvveti tarafından yapılan iş,

Uygulama noktasının hareket yönü, kuvvetle ayni yönde olmayıp bir q açısı gösterirse (Şekil-1) yapılan iş,

bağıntısı ile verilir. Kartezyan koordinatlardaki (X, Y, Z) kuvvet bileşenleri F_x, F_y, F_z ise, dw aşağıdaki eşitlikle gösterilir.

Bir kuvvetin yönü ve büyüklüğünün sabit olduğu koşulda Denklem(3)ün integrali yapılan işi (w) verir.

Şekil-1: İşin tanımlanması

ÖRNEK

Kütlesi m olan bir maddeye yerçekimi kuvvetinin etki ettiğini biliyoruz. Yeryüzünün çapı ile kıyaslandığında çok küçük kalan tüm mesafeler için F = mg dir. Böyle bir maddenin kaldırılması için yerçekimine karşı mg çarpımına eşit bir dış kuvvete gereksinim vardır. Kütlesi 1 kg olan bir maddeyi 1 m kaldırmak için yapılması gereken iş nedir?

w = mgr₁

w = 1 kg x 9.80 m/sn² x 1 m = 9.80 kgm/sn²

w = 9.80 newton metre (Nm) = 9.80 joule

Mekanik Enerji

Enerji sözcüğünü ilk kullanan bilim adamı d'Alambert'tir: "durgun haldeki bir maddenin enerjisi yoktur, oysa hareket halindeki madde belirli bir enerji içerir" (1785). Daha sonra Thomas Young enerjiyi "gerçek" ve "potansiyel" sözcükleriyle tanımladı. "Kinetik enerji" teriminin kullanılmasına ise çok daha sonra William Thomson ile başlanmıştır.

Bu gelişmeler Denklem(3)den başlayarak matematiksel olarak açıklanabilir. r₀ konumundaki bir tanecik F(r) kuvveti uygulanarak r₁ konumuna getirilsin; bu durumda yapılan iş,

Mesafeye bağlı integral, zamana bağlı integrale dönüştürülebilir.

Newton kuvvet kanunu (Denklem-1) uygulanarak aşağıdaki eşitlik çıkarılır.

Kinetik enerji, E = 1/2 mv² formülüyle tanımlandığından,

formülü elde edilir. Taneciğe yaptırılan iş, onun son ve ilk halleri arasındaki kinetik enerjiler arasındaki farka eşittir.

Denklem(8) deki kuvvet sadece r ye bağlı olduğundan, integral r nin diğer bir fonksiyonunu da tanımlar; bu, -dU(r) dir.

Bu eşitlik kullanılarak Denklem(8), aşağıdaki Denklem(10) şekline dönüşür.

Burada elde edilen U_(r) , "potansiyel enerji"dir. Potansiyel ve kinetik enerjiler toplamı (U + E_k), maddenin toplam mekanik enerjisidir ve bu toplam, sürtünmesiz hareket boyunca sabit kalır. Denklem(10), "enerjinin korunması" ilkesini gösterir. Örneğin, vakumda düşürülen bir maddenin kinetik enerjisinin artması, eşit miktarda potansiyel enerji kaybetmesiyle dengelenir.

Denge

Kimyasal deneylerde sadece belirli bazı taneciklerden değil, koşulları yönlendiren daha karmaşık "sistemler"den söz edilmelidir. Sistemler katı, sıvı ve gaz madde içerebilirler. Bir "sistem", hareketsiz bir alemden belirli sınırlarla ayrılmış bir parça olarak düşünülebilir. Ayrılan bu parçanın dışında kalan kısım onun "çevre"sidir. Sistemin sınırları, çevresindeki herhangi bir değişikliğin sisteme yansımasına izin vermezse, sistem "izole" edilmiş olur.

Bir sistemin özellikleri zaman içinde değişme eğilimi göstermiyorsa, sistem "denge hali"ne ulaşmıştır. Dengedeki bir sistem tekrarlanabilir niteliktedir ve "hal fonksiyonları" denilen bir seri özellikle tarif edilir; bunlar sistemin dengeye ulaşmadan önce geçirdiği durumlara bağlı değildir.

Denge kavramı basit bir mekanik modelle açıklanabilir. Şekil-2a'da bir kutunun masa üzerindeki üç değişik denge konumu görülmektedir. A ve C konumlarında kutunun ağırlık merkezleri diğer konumlardan daha aşağıdadır; bu nedenle küçük bir sarsıntı kutunun bu iki denge konumuna geçmesine sebep olur. A ve C konumlarında kutuların potansiyel enerjileri en düşük düzeydedir ve bu hallere "kararlı denge" halleri denir. Şekilde görüldüğü gibi C hali, A dan daha kararlıdır ve az bir kuvvetle kutu C konumuna geçmeyi yeğler. Kutunun A konumundaki haline "yarı karalı denge" hali denir. B konumu da bir denge halini gösterir, fakat bu "kararsız denge" halidir; bir sandalyenin iki ayağı üzerinde durdurulması bu hale örnek gösterilebilir. Kutunun B konumundaki ağırlık merkezi, diğer tüm konumlardaki halinden daha yüksektedir ve en küçük bir sarsıntı onun A veya C haline gelmesine neden olur.

Kararsız dengede potansiyel enerji maksimumdur; böyle bir dengeye ancak dengeyi bozabilecek hiçbir kuvvet bulunmadığı zaman ulaşılabilir.

Bu ilişkiler, sistemin potansiyel enerjisinin, Şekil-2a'daki ağırlık merkezlerinin fonksiyonu olarak grafiğe alınmasıyla daha kolay gözlenebilir (Şekil-2b). Kararlı denge hali eğride en düşük noktada bulunurken, kararsız denge hali en yüksek noktadadır. Herhangi bir sitemde kararlı ve kararsız denge konumları peşpeşe bulunur. Bir denge konumu için, potansiyel enerjinin yer değiştirmeye göre birinci türevi, yani eğrinin eğimi (dU / dr) sıfıra eşittir ve denge koşulu,

ifadesiyle verilir; ikinci türev dengenin kararlı veya kararsız olduğunu gösterir:

Şekil-2: Mekanik dengenin anlatımı

Maddenin Isıl Özellikleri

Bir maddenin dengedeki halinin hassas olarak tanımlanabilmesi için, ölçülen bazı özelliklerinin sayısal değerlerle verilmesi gerekir. Ancak özellikler arasındaki ilişkileri tarif eden bazı eşitlikler bulunduğundan, ölçülen her özelliğin belirtilmesi de gerekmez. Dış kuvvet alanlarının (çekim, elektromagnetik) ihmal edildiği ve maddenin bir gaz veya sıvı olduğunun varsayıldığı durumlarda, az sayıdaki özellik verileri maddenin halini tanımlayabilir (katıların özellikleri yöne göre karmaşık bir durum gösterir). Saf bir gaz veya sıvının halini tarif etmek için öncelikle onun her durumdaki kütlesi(m) belirlenmelidir. Bunun için de üç termodinamik değişken olan basınç(P), hacim(V) ve sıcaklık(q) üzerinde durulur. Bu özelliklerden ikisi sabit olduğunda, deneysel veriler üçüncünün de sabit kaldığını göstermiştir; yani, değişkenler arasında bir bağıntı bulunur. Diğer bir deyişle, P, V, q değişkenlerinden sadece ikisi bağımsız değişkendir. Maddenin halinin, P ve V ile tanımlandığının, fakat q nın kullanılmadığının özellikle bilinmesi gerekir.

İçinde sürtünmesiz bir piston olan bir silindirde bir miktar sıvı madde bulunsun (Şekil-3). Piston sıvının üzerindedir ve üstüne W = F = mg kuvvetinde bir ağırlık konmuştur. Sıvıya yapılan basınç,

eşitliğinden bulunur. Denge halindeyken bu basınç tüm sıvı boyunca tek bir değere ulaşır ve sıvı içindeki herhangi bir birim alanda sadece aynı P kuvveti hakim olur; başka bir deyişle basınç, her yöndeki düzgün bir gerginlik halidir.

Sıvı dengede olmadığı zaman pistonda dış basınçtan(P_ex) söz edilir. Fakat denge kuruluncaya kadar basınç sıvı içinde sürekli olarak değişir ve her noktada tek bir P değerine ulaşınca denge kurulur.

Bir sistemin özellikleri "yaygın" veya "yoğun" olarak sınıflandırılabilir. Yaygın özellikler birbirine eklenebilir; tüm sistem için değerleri, sistemdeki herbir kısım için olan değerlerinin toplamına eşittir. Bunlara "kapasite faktörleri" de denir. Örneğin, hacim ve kütle bu tip özelliklerdir. Yoğun özellikler veya "şiddet faktörleri" birbirine eklenemez; basınç ve sıcaklık gibi. Dengedeki bir sistemin küçük bir kısmının sıcaklığı, tüm sistemin sıcaklığına eşittir.

Sıcaklık q' yı fiziksel bir değer olarak kullanmadan önce, kantitatif olarak nasıl ölçüldüğünün bilinmesi gerekir.

Bir maddenin ısısı, yani sıcaklık veya soğukluk derecesi, onun sıcaklığıdır. Sıcaklık ölçmede "termometre"ler kullanılır. Bunlarda, belirli bir sıvının standardize edilmiş bir cam boru içindeki hacim değişikliği izlenir. Bu konudaki çalışmalar 1631 yılında başlamış ve çeşitli sıcaklık tarifleri yapılmıştır. 1710 yılında, su ile dengede olan buzun sıcaklığının 0 derece ve kaynayan suyun sıcaklığının da 100 derece olduğu kabul edilerek, standart cam borudaki civanın hacim değişikliği 100 eşit parçaya bölünmüş ve "santigrat skalası" veya "Celcius skalası" belirlenmiştir.

Şekil-3: Bir sıvı içindeki basıncın tanımlanması; sıvıdaki çekim alanı, yani sıvının kendi ağırlığı ihmal edilmiştir.

Boyle Kanunu

Civalı barometre Toriçelli tarafından keşfedilmiştir (1643). Atmosfer basıncındaki kolonun yüksekliği günden güne bir kaç cm civa seviyesinde değişebilir. Fakat "standart atmosfer", bir metre kare için 101325 Newton’a eşit bir basınçtır (N/m²). Yüksek basınçlar çoğu kez kilobar (kbar=10⁸ N/m²) ile, düşük basınçlar torr (atm/760) ile verilir.

Robert Boyle ve arkadaşları bir gazın basıncını bir hava yayına benzetmişlerdir. Bir hacim gaz bir pistonla silindir içine sıkıştırılabilir. Ancak piston üzerindeki kuvvet kaldırıldığında, gaz pistonu yay gibi davranarak geri iter.

Şekil-4 deki gibi, içinde civa bulunan ve bir ucu kapalı olan J tüpüne açık uçtan civa ilave edildiğinde kapalı uçtaki gazın basıncı artar, hacmi azalır.

Bu deney basıncın artmasıyla orantılı olarak hacmin azaldığını, fakat gazın sıcaklığının sabit kaldığını gösterir. Boyle Kanunu: "Sabit sıcaklıktaki bir gazın hacmi, basıncıyla ters orantılıdır" şeklinde tarif edilir ve aşağıdaki gibi yazılır (C orantı sabitidir).

Denklem(11)e Boyle Kanunu denir. Kanun orta derecelerdeki basınçlarda geçerlidir, ancak yüksek basınçlarda sapmalar olur.

Şekil-4: Boyle J tüpü.

Gay - Lussac Kanunu

Gazların hacimleri sıcaklıkla önemli derecelerde değişiklik gösterir. Bu konudaki ilk çalışmaları 1802-1806 yılları arasında Joseph Gay-Lussac yapmıştır. çalışmaları azot, oksijen ve hidrojen gibi "kararlı gazlar"la tekrarlayarak farklı gazların hacimlerinin (V), sıcaklığa (q) aynı derecede bağımlı olduğunu bulmuştur. Gay-Lussac'ın elde ettiği sonuçlar matematiksel olarak açıklanabilir. Gazların V hacminin q sıcaklığıyla doğrusal olarak değiştiğini kabul edelim. Bir gazın 0 ⁰C deki hacmi V₀ ise,

a₀ katsayısı "ısıl genleşme" veya "ısıl genleşme katsayısı"dır. Gay-Lussac a’nın yaklaşık olarak 1/267 ye eşit olduğunu bulmuştur. Ancak Regnault (1847) a’yı daha hassas tayin ederek 1/273 e eşit olduğunu saptamıştır. Bu değer kullanıldığında Denklem(11) aşağıdaki şekilde yazılır.

Bu bağıntıya "Gay-Lussac Kanunu" denir; "sabit basınçtaki bir gazın sıcaklığı bir derece arttığında hacmi, 0 ⁰C deki hacminin 1/273 katı kadar artar".

Gerçek gazlar Boyle ve Gay-Lussac kanunlarına uymazlar; gazın yüksek sıcaklıkta ve düşük basınçta olması sapmayı azaltır. Sapma gaza göre de değişir; örneğin, helyumda az, karbon dioksitte fazladır. Bu kanunlara tam olarak uyan gazlara "ideal gazlar" denir. Gazlar düşük basınçlarda (yoğunlukları da düşüktür) kanunlara daha yakındırlar. Bu nedenle gerçek gazların ölçüm değerleri sıfır basınca ektrapole edilerek ideal gaz özellikleri elde edilir.

Şekil-5 te azot, H₂ ve He’un a₀ değerleri görülmektedir. Sıfır basınçta her üçü için de aynı a₀ değeri elde edilir; bu ise ideal bir gazın değerine eşittir.

Buna göre ideal bir gaz için Gay-Lussac kanunu,

eşitliği ile verilir. Burada yeni bir sıcaklık skalası tarifine gereksinim vardır; T = mutlak sıcaklıktır ve birimi Kelvin, K dir. Böylece, T = q +T₀ olduğundan, Gay-Lussac Kanunu aşağıdaki şekilde yazılabilir.

Şekil-5: Isıl genleşme katsayılarının sıfır basınca ekstrapolasyonu

Mol Tanımları

"Bir maddenin miktarı" önemli bir fizikokimyasal değerdir. Madde miktarının SI birimi "mol"dür. Mol, karbon atomunun tam olarak 0.012 kg karbon-12 olduğu varsayıldığında, çeşitli elementer birimlerden oluşan bir sistemin miktarını gösterir. Elementer birim bir atom, bir molekül, bir iyon, bir elektron, bir foton, v.s. veya belirlenmiş bir grup olabilir.

Örneğin, 1 mol Hg Cl nin kütlesi, 0.23604 kg; 1 mol Hg₂ Cl₂ nin kütlesi, 0.47208 kg; 1 mol Hg nın kütlesi, 0.20059 kg; 1 mol Cu_0.5 Zn_0.5 in kütlesi, 0.06446 kg; 1 mol Fe_0.91 S in kütlesi, 0.08288 kg; 1 mol e^- un kütlesi, 5.4860 x 10^-7 kg; 1 mol (%78.09 mol N₂ + %20.95 mol O₂ + %0.93 mol Ar + %0.03 mol CO₂) in kütlesi, 0.028964 kg dır.

İdeal Bir Gazın Hal Denklemi

P, V, T değişkenlerinden herhangi iki tanesi, belirli miktardaki bir gazın halini tanımlar ve üçüncü değişkeni de sabit tutar. Denklem(11) sabit T de P nin V ile, Denklem(14) de sabit P de V nin T ile olan değişiklilerini göstermektedir.

Bu iki eşitlik birleştirilebilir; şöyle ki, gazın ilk bulunduğu hal P₀, V₀, T₀ ile, ikinci hal de P, V, T ile gösterilsin. Gaz ilk haldeyken T₀ sabit tutularak basınç P ye yükseltilir; bu durumda hacim V_x gibi bir değere değişir. Sonraki aşamada P sabit tutulur ve sıcaklık T₀ dan T değerine çıkarılır, hacim ise V değerine gelir.

İdeal bir mol gaz için P₀ = 1 atm, T₀ = 273.15 K dir. Bu koşullarda V₀ = 22414 cm³/mol (V₀/n) dür. Avagadro Kanununa göre bu hacim tüm ideal gazlar için geçerlidir. n mol ideal gaz için,

R ye "her mol için gaz sabiti" denir. Bu eşitlik "ideal bir gazın hal denklemi" olarak bilinir. Denklem üç kanunu birarada içermektedir; Boyle, Gay-Lussac, ve Avagadro kanunları. İdeal gaz sabiti R çeşitli birimlerle verilebilir, bazıları Tablo-1’de gösterilmiştir.

Denklem(16), bir gazın yoğunluğundan molar kütlesinin(M) hesaplanmasına olanak verir. Hacmi V olan bir gazın kütlesi m ise, r yoğunluğu ve n miktarından, Denklem(16) kullanılarak M değeri bulunur.

 

Tablo-1: İdeal Gaz Sabiti R’nin Çeşitli Birimlere
Göre Değerleri

Hal Denklemi ve PVT İlişkileri

Bağımsız değişkenler olarak P ve V seçildiğinde, n miktardaki saf bir maddenin sıcaklığı P ve V nin fonksiyonu olur. V_m =V/n ise,

T nin sabit bir değeri için, bu eşitlik bir izotermi tarif eder. Isıl dengede, bir maddenin hali, üç değişken olan basınç, molar hacim ve sıcaklıktan herhangi ikisinin belirlenmesiyle sabitleştirilir; sonra üçüncü değişken, Denklem(17) nin çözülmesiyle bulunur. Denklem(17) "hal denklemi"nin genel ifadesidir ve özel bir bağımsız değişken olmadığında, (P, V_m, T) = 0; örneğin, (P V – n RT) = 0.

Geometrik olarak düşünüldüğünde, denge halindeki saf bir sıvı P, V, T ile gösterilen üç boyutlu bir yüzeydir. Şekil-6a’da ideal bir gaz için böyle bir PVT yüzeyi görülmektedir. Sabit sıcaklıktaki noktaların birleştirilmesiyle elde edilen izotermal hatlar PV düzleminde bulunur (Şekil-6b). Sabit hacim hatları PT düzlemindedir ve "izokorlar" veya "izometrikler" adını alır (Şekil-6c). İdeal olmayan bir gazda bu hatlar düz değildir. Sabit basınç hatlarına "izobarlar" denir.

İzobarik bir eğrinin eğimi, seçilen sabit bir basınçta sıcaklıkla hacmin değişme hızını verir. Bu nedenle eğim (¶V / ¶T)_p şeklinde gösterilir. Burada kısmi türev alınmasının nedeni, V nin T ve P nin fonksiyonu olmasıdır. V nin T ile değişme fonksiyonu a ile gösterilir ve "ısıl genleşme" olarak tanımlanır, birimi 1/T dir.

Şekil-6: (a) Bir ideal gaz için PVT yüzeyi; kesiksiz çizgiler izomerler, kesikli çizgiler izobarlar, noktalı çizgiler izometriklerdir. (b) PVT yüzeyinin PV düzlemindeki görünümü; izotermleri gösterir. (c) PVT yüzeyinin PT düzlemindeki görünümü; izometrikleri gösterir.

Benzer şekilde izotermal bir eğrinin eğimi, sabit sıcaklıkta basınçla hacmin değişmesini verir. Bu değişiklik b terimi ile gösterilir ve bir maddenin "izotermal sıkıştırılabilmesi"ni tanımlar. Negatif işaret, basınç artmasının hacim azalmasına neden olmasından dolayıdır; bu durumda (¶V / ¶T)_T negatif olur; b birimi 1/P dir.

Hacim hem T nin hem de P nin fonksiyonu olduğundan, diferensiyal bir değişiklik(dv) aşağıdaki şekilde gösterilir.

Denklem(20), Şekil-7'deki grafikle gösterilir; burada dikey eksen V dir ve PVT yüzeyinin bir kısmı verilmiştir. abcd alanı, yüzey alanının bölünemeyecek kadar küçük bir parçasıdır; VT ve VP düzlemlerine paralel düzlemlerle yüzeyden kesilerek elde edilmiştir. Gaz a noktasındayken hal değişkenleri V_a, P_a, T_a dır. P ve T bölünemeyecek kadar küçük miktarlarda değiştirilerek P + dP ve T + dT yapıldığında sistem c noktasıyla gösterilen hale gelir ve V deki değişiklik dV,

V_b – V_a, P nin sabit olduğu ve sadece sıcaklığın değiştirildiği durumda V deki değişikliktir. Bu nedenle ab nin eğimi (P = sabit),

V_b – V_a nın bölünemeyecek kadar küçük miktarda değişmesi (¶V / ¶T)_p dT dir. Aynı şekilde V_c – V_b, (¶V / ¶P)_T dP dir. V deki toplam değişiklik, Denklem(20)de görüldüğü gibi bu iki kısmi değişikliğin toplamıdır.

Kısmi diferansiyel katsayılar (a ve b) arasında ilginç bağıntılar elde edilebilir. Denklem(20)nin çözümüyle dP bağıntısı çıkarılır.

Keza, Denklem(20) ye benzer olarak dP için aşağıdaki genel eşitlik de geçerlidir.

dT’nin katsayıları birbirine eşit olacağından,

(¶P / ¶T)_V’nin a / b’ya eşit olduğu görülür.

ÖRNEK

Laboratuvarlarda çok karşılaşılan bir olay, civalı cam termometrelerin aşırı ısınma halinde kırılmasıdır. Bir termometre 50 ⁰C de civa ile tamamen doldurulmuşsa, 52 ⁰C ye ısıtıldığında ne kadar basınç meydana gelir? Bu koşullardaki civa için a =1.8x10⁰⁴ 1/⁰C, b = 3.9x10^-6 1/atm dir.

Görülüyor ki 46 atmosfere dayanabilen cam boru, 92 atmosfer gibi bir basınçla karşılaşmaktadır. Bu durumda termometrenin kırılması sürpriz olmamalıdır.

Gerçek Gazların PVT Davranışı

Gazlar, sıvılar ve katıların basınç, hacim, sıcaklık (PVT) ilişkileri genel olarak Denklem(17) ile tarif edilir. Ancak, sadece gazlar için önemli hal denklemleri çıkarılabilmiştir.

İdeal gaz denklemi PV = n RT, bir yaklaştırma yapılarak gerçek gazlara da uygulanabilir. Bir gazın ideallikten sapmasını gösteren uygun bir yol, ideal gaz denklemine "sıkıştırılabilme faktörü" denilen bir z faktörü konulmasıdır.

z faktörüne "sıkıştırılabilme faktörü" denir. İdeal bir gaz için z = 1 dir. Gaz ideallikten ayrıldıkça z değeri 1 den sapar. İdeallikten sapma sıcaklık ve basınca bağlıdır; yani z, T ve P nin bir fonksiyonudur. Şekil-8 de bazı sıkıştırılabilme faktörü (T = 0 ⁰C de) eğrileri görülmektedir; bunlar değişik basınçlarda maddelerin hacimlerinin ölçülmesiyle yapılan verilere göre çizilmiştir. (NH₃ ve C₂ H₄, yüksek basınçlarda sıvı maddelerdir.)

Şekil-8: Sıkıştırılabilme faktörleri; z = PV / n RT, 0 ⁰C’de

Uygun Haller Kanunu

Belirli bir sıcaklık ve basınçta, buharı ile dengede olan bir sıvının denge basıncına, bu sıvının "buhar basıncı" denir. Sıvı buhardan daha yoğundur.

Böyle bir sistem kapalı ve şeffaf bir tüp içinde ise, sıvı ve buharı arasında iki fazın varlığını gösteren bir menisküs gözlenir. Ancak, her maddeye özgü olan ve kritik sıcaklık (T_c) denilen bir sıcaklığın üstünde sisteme ne kadar basınç uygulanırsa uygulansın tek faz bulunur. T_c değerinin üstündeki sıcaklılarda madde "akışkan (mayi) halde"dir. Akışkanı T_c de sıvılaştıran basınç "kritik basınç (P_c)" tır. Maddenin T_c ve P_c de kapladığı molar hacim de "kritik hacim", V_c dir. Bazı maddelerin kritik değerleri Tablo-2 de görülmektedir.

P, V, T değerleri P_c, V_c, T_c kritik değerlerine bölündüğünde "indirgenmiş" basınç, hacim, sıcaklık değerleri elde edilir.

van der Waals, özellikle orta basınçlarda, hal değişkenleri P_R, V_R, T_R ile tanımlandığında [V_R =f (P_R; T_R) gibi] tüm gazların ayni hal denklemine uygunluk gösterdiğini ileri sürmüş ve bu kurala "Uygun Haller Kanunu" adını vermiştir. Bu kanun doğru ise, tüm gazların kritik oranı P_c V_c / RT_c nin ayni olması gerekir Gerçekten de Tablo-2 deki değerlerden hesaplandığında bu oranın sadece 3-5 gibi bir aralıkta değiştiği görülür.

Sıkıştırılabilme faktörü z ile indirgenmiş P_R ve T_R değerleri arasında, yüksek basınçlarda bile, ilginç bir bağıntı bulunur; z, P_R ve T_R nin bir fonksiyonudur.

z nin P ve T ile değişimi (z = PV/RT), PV ye karşı grafiğe alındığında Şekil-9 daki eğriler elde edilir. Kimya mühendisleri ve araştırmacılar gazların yüksek basınçlardaki özelliklerini incelerken bu grafiklerden yararlanırlar.

Tablo-2: Kritik Nokta Verileri ve 
van der Waals Sabitleri

Şekil-9: İndirgenmiş hal değişkenlerinin fonksiyonu olarak sıkıştırılabilme faktörleri

Gazların Hal Denklemleri

Hal denklemi indirgenmiş değişkenlerle yazılırsa, F (P_R, V_R) = T_R gibi, en az iki bağımsız sabit içerecektir; örneğin P_c ve V_c gibi. İdeal gaz denkleminden daha doğru PVT verilerinin elde edildiği çok sayıda hal denklemi vardır. Bunlardan en çok bilinen ikisi aşağıda verilmiştir.

Örneğin, van der Waals denklemi:

D. Bertholet denklemi:

van der Waals denklemiyle, ideallikten orta derecedeki sapmalarda doğruya çok yakın PVT verileri elde edilir.

Kritik Bölge

Bir gazın kritik bölge yakınındaki davranışı, ilk defa Thomas Andrews tarafından incelenmiştir (1869). Andrews karbon dioksit ile bir dizi deneyler yapmıştır. 1937 de A. Michels ve arkadaşları karbon dioksitin kritik sıcaklık 31.01 ⁰C dolayındaki PV izotermlerini içeren bir yayın çıkarmışlardır (Şekil-10).

Şekil-10 daki 30.4 ⁰C izoterminde (T_c den düşüktür) PV eğrisi Önce AB yolunu izler, bu yaklaşık olarak bir Boyle kanunu izotermidir. B noktasına ulaşıldığında bir menisküs meydana gelir ve sıvı oluşumu başlar. C noktasına kadar sabit basınçta sıkışma devam eder; bu noktada tüm gaz sıvı hale dönüşmüştür. CD eğrisi sıvı karbon dioksitin izotermidir; eğrinin dikliği sıvının sıkıştırılabilme özelliğinin düşük olduğunu gösterir. Daha yüksek sıcaklıklardaki izotermlere doğru gidildiğinde, 31.01 ⁰C izotermine ulaşılıncaya kadar B ve C noktalarının birbirine yaklaştığı görülür. 31.01 ⁰C izotermi, karbon dioksitin kritik sıcaklıktaki izotermidir. Bu sıcaklığın üstündeki izotermler, ne kadar yüksek basınç uygulanırsa uygulansın ikinci bir faz oluşumu göstermezler.

Kritik sıcaklığın üstünde tam bir "devamlı haller" bulunduğundan, sıvı ve gaz arasında herhangi bir ayırım yapılamaz. Bu durum EFGH yolunu izleyerek gösterilebilir. Sıcaklığı T_c den daha düşük olan E noktasındaki gaz sabit hacimde ısıtıldığında, T_c den daha yüksek sıcaklıktaki F noktasına gelir. Sonra FG izotermi boyunca sıkıştırılır ve sabit hacimde GH yoluyla soğutularak H noktasına getirilir; bu noktanın sıcaklığı T_c den düşüktür. Karbon dioksit H de sıvı haldedir, fakat izlenen bu yol boyunca hiç bir zaman iki faz (sıvı ve gaz) bir arada bulunamaz. Gaz halinden sıvı haline geçiş düzgün ve süreklidir.

Van Der Waals Denklemi ve Gazların Sıvılaştırılması

van der Waals denklemİ, ideal halden sadece orta derecelerde sapmalar gösteren gazlar İçİn oldukça doğru PVT verileri verir. Şekil-10 da kesikli çizgilerle gösterilen eğriler ideal halden sapmaları, yani van der Waals izotermlerini göstermektedir. van der Waals denklemi homojen gazlar ve hatta homojen sıvılar için bile daha iyi sonuçlar verir. van der Waals izotermi sıvılaşma süreci boyunca sabit bir basınç göstermez, bir maksimum ve bir minimum verir. Sıcaklığın kritik değere doğru yükselmesi bu maksimum ve minimumun birbirine yaklaşmasına yol açar. Kritik değerde bu iki nokta PV eğrisinin dönüm noktası halini alır.

Şekil-10: Karbon dioksitin kritik bölge yakınındaki izotermleri

Bir maksimum için analitik koşul:

Bir minimum için analitik koşul:

van der Waals denklemine göre, 1 mol (n = 1) gaz için, kritik noktada (T = T_c, V = V_c, P = P_c) aşağıdaki üç denklem aynı anda geçerlidir.

Eşitlikler kritik sabitleri içerecek şekilde çözüldüğünde, T_c, V_c, P_c bulunur.

R tüm gazlar için sadece a ve b ye bağlıdır ve aşağıdaki denklem çıkarılır.

İndirgenmiş hal değişkenleri P_R, V_R, T_R kullanılarak da van der Waals denklemi yazılabilir. Şöyle ki,

Bertholet denklemi 1 atm basınçta, aşağıdaki şekliyle kullanılır.

İdeal Gaz Karışımları

Bir karışım n₁, n₂, ...n_j...n_c miktarlarda maddeler içeriyorsa, toplam miktar,

denklemi ile verilir. Karışımın bileşimi, her bir maddenin mol kesrinin belirtilmesiyle tarif edilir; örneğin j maddesinin mol kesri,

Karışımın bileşimini tanımlayan diğer bir kavram da konsantrasyondur.

İncelenen sistem bir gaz karışımı ise, karışımda bulunan her bir bileşenin "kısmi basınç"ından söz edilir; P₁, P₂, ...P_j... gibi. Bileşenin konsantrasyonu bilinirse, PVT verilerinden veya hal denkleminden kısmi basıncı bulunabilir.

Her bir bileşenin ideal bir gaz gibi davrandığı,

durumunda bile birbirine benzemeyen gazlar arasındaki etkileşim ΣP_j nin P den biraz farklı olmasına yol açar. Bu nedenle "ideal gaz karışımı",

Bu denkleme "Dalton Kısmi Basınçlar Kanunu" denir.

Her gazın ideal bir gaz gibi davrandığı karışım, "ideal gazların ideal bir karışımı"dır.

eşitliği bulunur. Buna göre, ideal bir gaz karışımındaki herbir gazın kısmi basıncı, kendi mol kesri ile karışımın toplam basıncının çarpımına eşittir. Sabit bileşimdeki bir gaz karışımının PVT davranışı, karışımın saf ve tek bir madde olduğu varsayılarak tayin edilir. Elde edilen veriler bir hal denklemine uygulanarak parametreler hesaplanır. Bulunan değerler karışımın bileşimine bağlı parametre değerleridir.

Isı ve Isı Kapasitesi Kavramları

"Sıcaklık" olayını açıklayan deneysel gözlemler ayni zamanda "ısı" kavramını da açıklar. Fakat çoğu zaman bu iki kavram birbirine karıştırılmaktadır.

"Sıcaklık" yoğun (intensive), "ısı miktarı" yaygın (extensive) özelliklerdir. Yaygın özellikler toplanabilir, yoğun özellikler ise toplanamazlar (sıcaklık, basınç).

Joseph Black "kalorimetre" ile yaptığı ve 1803 te yayınladığı çalışmasında, ısının bir madde gibi davrandığını, bir ortamdan bir diğerine geçebildiğini, fakat toplamının daima sabit kaldığını kabul etmiştir. Bu görüş diğer araştırmacılar tarafından da benimsenmiştir. Tipik bir örnekle konu daha iyi anlaşılabilir. Kütlesi m₂, sıcaklığı T₂ olan küçük bir kütle, içinde kütlesi m₁, sıcaklığı T₁ olan su bulunan bir kap içine konulsun. Bu durumda bulunması gereken koşullar: (1) sistem çevresinden izole edilmiştir, (2) kap içinde herhangi bir değişiklik olmayacağı varsayılmıştır, (3) buharlaşma, ergime, çözünme veya kimyasal reaksiyonların bulunmadığı kabul edilmiştir. Bu koşullarda, sistem T gibi yeni bir sıcaklığa ulaşır; T, T₁ ve T₂ arasında bir değerdir ve sıcaklıklar arasında aşağıdaki denklemle verilen bir eşitlik bulunur.

Burada c₂ metalin "öz (spesifik) ısı"sı, C₂ = c₂ m₂ deneyde kullanılan metalin "ısı kapasitesi"dir. Ayni şekilde, suyun öz ısısı c₁, kullanılan suyun ısı kapasitesi C₁ = c₁ m₁ dir. Öz ısı, birim kütlenin ısı kapasitesidir.

Denklem(36), Denklem(10) dakine benzer bir korunma denklemidir. Yapılan deney koşullarında ısının korunduğu ve sıcaklıkları eşitleninceye kadar daha sıcak ortamdan daha soğuk olana doğru aktığı düşünülebilir. Akan ısı q,

"Isı birimi" gram kaloridir (g kal) ve bir gram suyun sıcaklığını 1 ⁰C yükseltmek için absorblanması gereken ısı miktarı olarak tarif edilir.

Öz ısı sıcaklığın bir fonksiyonudur. Bu durumda kalorinin, sıcaklık ta belirtilerek daha hassas bir tarifi yapılmalıdır. Standart olarak 15 ⁰C deki kalori alınmıştır; 1 kalori, 1 g suyun sıcaklığını 14.5 ⁰C den 15.5 ⁰C ye çıkarmak için verilmesi gereken ısı miktarıdır. Isı kapasitesi sıcaklığın bir fonksiyonu olduğundan, diferensiyal bir ısı akışı dq ve sıcaklık değişimi dt ile hassas olarak tarif edilir.

Hacim Değişmesinde Yapılan İş

Isı transfer deneyinde sistemin tamamen izole olduğu ve çevresiyle herhangi bir mekanik etkileşimde bulunmadığı kabul edilmişti. Bu sınırlamalar olmadığında, sistem ya çevresinde veya kendinde iş yapar. Her iki durumda da bir maddeye ilave edilen ısının sadece bir kısmı onun sıcaklığını yükseltirken, kalan kısım maddenin yaptığı işe harcanır.

Diferensiyal iş Denklem(3)de dw = F dr şeklinde tarif edilmişti. İş, kuvvet ile kuvvetin uygulandığı noktanın kuvvet yönündeki yer değiştirmesinin çarpımıdır. Şekil-3 deki sistem sürtünmesiz hareket eden bir pistonun bulunduğu ve bir sıvı içeren termodinamik bir sistemdir. Alanı A olan piston üzerindeki dış basınç P_ex = F/A dır. Piston F kuvveti yönünde dr kadar hareket ettiğinde yapılan iş,

Buradaki iş, kuvvet tarafından yapılan iştir. Mekanik olaylarda iş daima kuvvetle ilişkilidir. Kuvvetin bir kütle noktasına, bİr kütle noktaları toplamına, sürekli bir ortama veya sisteme uygulanması önem taşımaz, uygulandığı noktanın yer değiştirmesi işin hesaplanması için yeterlidir. Termodinamikte sistem ve çevresi önemlidir. "Sistemde" ve "sistemden"" yapılan işler vardır. Sistemde yapılan iş (+), sistemden çevreye yapılan iş ise (-) işaretle gösterilir; buna göre sistemde yapılan iş,

Buradaki negatif işaret, sıkıştırmada dV nin negatif olmasındandır. P_ex, sistemde iş yapılabilmesi için uygulanan dış basınçtır. Sistemin bu dış basınçla dengede olması gerekmez. Sistem V₁ den V₂ ye kadar sıkıştırıldığında basınç sabit tutulursa, sıvı üzerinde yapılan iş Denklem(38)den hesaplanır.

Dış basıncın ardarda gelen her noktada (genişleme veya sıkışma) bilindiği bir hacim değişikliğinde, P_ex değerleri V değerlerine karşı grafiğe alınabilir. Böyle bir grafiğe "indikatör diyagramı" denir. Şekil-11a da görülen örnekte sistem tarafından yapılan iş eğrinin altındaki alana eşittir.

A noktasından B noktasına gidilirken yapılan iş geçiş yoluna bağlıdır. Örneğin, A dan B ye Şekil-11b deki gibi iki değişik yoldan gidilsin. ADB yolunda, ACB yolunun izlenmesinde olduğundan daha fazla iş yapılır; çünkü ADB nin altındaki alan ACB nin altındakinden daha büyüktür. Eğer ADB yoluyla B ye ulaşılıp, buradan da BCA yoluyla tekrar A ya dönülürse tamamlanmış bir "halkalı işlem" yapılmış olur; sistemin yaptığı net iş, eğrilerin altındaki alanların farkına eşittir.

Termodinamik yorumlarda, sistemden veya çevresinden sözcüklerini kullanırken neyin tarif edilmek istendiğinin çok iyi bilinmesi gerekir. Şekil-3 deki örnekte pistonun ağırlığının olmadığı ve sürtünmesiz çalıştığı varsayılmıştı. Bu durumda, sistem gazdır, piston ve silindir ise gazı çevreleyen ideal sınırlardır. Gerçek bir silindir ve sürtünmeli bir pistonun olduğu halde ise piston ve silindirin sistemin bir parçası mı yoksa çevrenin bir parçası mı olduğunun dikkatli bir şekilde belirtilmesi gerekir. Pistonda çok fazla iş yapılırken bunun sadece bir kısmı gaza iletilir, kalan kısım piston tarafından sürtünme ısısı olarak harcanır.

P_ex - V eğrisi boyunca ardarda gelen her nokta sistemin bir denge hali ise, çok özel bir durum olan P_ex = P eşitliği gerçekleşir; P sıvının kendi basıncıdır.

Şekil-11: PV işi için indikatör diyagramı; (a) A’dan B’ye giden genel bir işlem, (b) bir ADBCA halkalı sistem. (c) Dengede bir mayi içeren bir sistemde yapılan işin indikatör diyagramı; P_ex = P

İndikatatör eğri, bu durumda sistemin denge eğrisi olur. Böyle bir durum Şekil-11 (c)’ de görülmektedir. Sadece denge hali devam ettiğinde, işin hesabı maddenin kendi hal fonksiyonlarından (P ve V) yapılabilir.

Genel İş Kavramı

Mekanik sistemlerde iş daima iki terimin çarpımı olarak verilir; yoğun bir faktör olan kuvvet ve yaygın bir faktör olan yer değiştirme. Mekanik olmayan iş tanımlarında da böyle bir formülasyon uygulanır.

Fizikokimyada elektrik hücrelerinde oluşan değişiklikler geniş bir inceleme konusudur. Elektriksel iş de kuvvet hücrenin elektromotor kuvvetidir (emf) ve E ile gösterilir. Yer değiştirme de hücre deşarj olurken (dQ < 0) dış devre boyunca transfer olan şarjdır (dQ). Magnetik bir durumda ise yoğun faktör magnetik alan kuvveti, H dir. Bu alan bir maddeye etki ederek alan yönünde bir dM magnetikliği yarattığında madde üzerinde yapılan iş HdM ye eşit olur. Çeşitli iş tanımları Tablo-3 de gösterilmiştir.

Tersinir İşlemler (Prosesler)

Şekil-11 (c)'de görülen PV diyagramında izlenen yol özel bir durumu belirtir ve termodinamik anlamda çok önemlidir; buna "tersinir yol" denir. Tersinir bir yol, denge halindeki tüm ara halleri bağlayan tek yoldur. Böyle bir denge yolu boyunca ilerleyen işlem "tersinir işlem"dir. Örneğin, bir gazın tersinir genleşmesinde piston üzerindeki basınç sonsuz derecede yavaş kalkmalıdır. Bu durumda gaz hacminin her yerindeki basınç daima ayni ve piston üzerindeki zıt basınca eşit olur. Sadece böyle bir koşuldaki gazın hali P ve V hal değişkenleriyle tanımlanabilir. (Tersinmez hal, indikatör diyagramında P_ex in V ye karşı grafiğe alınmasıyla gösterilir. Sadece tersinir durumda P_ex = P dir, bu hal maddenin kendi özelliğinden kaynaklanır.) Geometrik terimlerle ifade edildiğinde gazın hali PV düzlemindeki bir nokta ile gösterilir. Böyle noktaları birleştiren hat, bir denge noktaları birleştirme hattıdır. Piston aniden geri çekildiğinde gaz hızla boş yerleri doldurmaya çabalar, gaz hacmi boyunca basınç farkları oluşur, hatta türbülens bir hal meydana gelir. Bu koşuldaki bir gazın hali P ve V değişkenleri ile tanımlanamaz.

Çeşitli noktalarda çeşitli basınçlar bulunacağından çok sayıda değişken bulunur. Bu tür bir hızlı genişleme tipik bir "tersinmez işlem"dir; ara haller dengede değildir.

Tersinir işlemler sonsuz yavaş ilerleyebilen işlemler olduğundan gerçekleşemezler. Bu nedenle doğal işlemlerin tümü tersinmezdir. Tersinir yol, tersinmez bir işlemin denge koşullarına çok yakın koşullarda yapılması halinde ulaşılan sınır yoldur. Gerçek bir tersinirlik sağlanamamasına rağmen tersinir yol tam olarak tanımlanabilir ve bu yol boyunca yapılan iş hesaplanır. Ancak, tersinirlik koşullarında yine de deneylerde yaklaştırmalar yapılır.

Şekil-11 (c) de A dan B ye giden bir yol gösterilmiş olmasına rağmen, B ye farklı yollardan da ulaşılır. Çünkü hacim V, basınç P nin olduğu gibi sıcaklık T’nin de bir fonksiyonudur. İşlem boyunca tek bir sıcaklık seçilir ve sabit tutulursa sadece bir tersinir yol olasıdır. Böyle bir "izotermal koşul"da A dan B ye tersinir bir yol ile giden sistem üzerinde yapılan iş, seçilen sıcaklık için "minimum iş" olarak tarif edilir. Bu yorum doğrudur, çünkü tersinir durumda genişleme en yüksek zıt kuvvete karşıdır; zıt kuvvet ise itme kuvveti ile dengededir.

Tablo-3: Çeşitli İş Tanımları

GERİ (proje çalışmaları)