Kulomb (Coulomb, C), elektrik yükünün veya miktarının birimi "kulomb"dur
(C). Bir kulomb, 0.00111800 g gümüş iyonunun gümüş metaline dönüşmesi için gereken
yüktür.
Diğer bir birim "faraday" dır (F), ve bir eşdeğer
yükü gösterir, 1F = 6.02 x 1023
yüklü taneciktir. İki birim arasındaki ilişki, tariflerinden
yararlanılarak çıkarılır.
Elektrik akımı I, bir yükün akış hızıdır, ve aşağıdaki eşitlikle verilir.
dQ
I =¾¾ (1)
dt
Q yüktür. Akım birimi "amper" (A), bir kulonun saniyedeki hızı olarak tarif edilir.
Volt (V), mekandaki iki nokta arasındaki elektrik potansiyeli (V), bir elektrik yükünün bir noktadan diğer bir noktaya hareketi için gerekene iştir. İşin jul, yükün kulomb cinsinden verilmesi durumunda, potansiyelin birimi "volt" olur. Yani, 1 volt her bir kulomb için 1 julü gösterir.
1 (kg m2
1 V = ¾¾¾¾
s3 A
Direnç (R) birimi "ohm" (W), 1 volt potansiyelin 1 amper akım üretmesine karşı gösterilen direnç olarak tarif edilir.
volt
Ohm = ¾¾¾¾
amper
Elektrik iletkenliği (G), direncin tersi olan bir ifadedir ve birimi "ters Ohm" (W-1), veya simens (S) tir.
amper
S = ¾¾¾¾
volt
Elektrik gücü (P), jul/saniye veya "Watt" (W) cinsinden elektriksel işin hızıdır. Elektronların geçişi sırasında harcanan güç,
P = I V (2)
denklemiyle verilir. Denklem(4) ün (2) de yerine konulmasıyla aşağıda eşitlik çıkarılır.
V2
P = I2 R = ¾¾ (3)
R
Henry (H), indüktans birimidir; saniyede bir amper şiddeti ile değişen bir devredeki akimin ürettiği bir voltluk elektromotor kuvvetinin indüktansına eşittir.
1 kg m2
1 H = ¾¾¾¾
s2 A-2
Hertz (Hz), frekansın, saniyede bir devire eşit olan birimidir, alternatif akımda, pozitif ve negatif kutupların bir saniyedeki değişim sayısıdır.
Potansiyelleri farklı iki nokta arasında bir iletim yolu bulunuyorsa, potansiyel farkı sıfır oluncaya kadar yük akar. Örneğin, Şekil-1’de görülen doğru akım devresinde düğme kapatıldığında, bir iletim yolu oluşur, bu yol boyunca bataryanın bir ucundan (terminalinden) diğerine doğru yük akışı başlar, A ve B arasındaki potansiyel farkı sıfır oluncaya kadar da devam eder; bu noktada batarya boşalmış, yani deşarj olmuştur.
"Konveksiyon"la (dolaşımla), bir akımın yönü daima pozitif uçtan negatif uca doğrudur. Yön, akımı taşıyan taneciğin tipine bağlı değildir. Buna göre Şekil-1’deki dış devrede akımı, BC ve AD metal iletkenlerindeki elektronların hareketi oluşturur. Akımın (I) yönü A dan D ye C ye B’ye doğrudur; yani akım, daima, pozitif yükün hareketiymiş gibi görünür.
Şekil-1: Bir doğru akım devrede iletim
İki platin elektrot (C ve D) ve daldırıldıkları seyreltik sülfürik asit çözeltisiyle bir elektrokimyasal hücre oluşur. Bu hücreden elektrik geçişi, metalik iletkenden tamimiyle farklı bir mekanizmayla olur. Burada pozitif hidrojen iyonları C elektrotuna doğru, negatif sülfat ve hidrojen sülfat iyonları da D elektrotuna doğru göç ederler; akım bu iki göç olayına göre oluşur. Anyonik göç ile D’nin etrafında toplanma eğiliminde olan fazla negatif yük, bu elektrotta üretilen pozitif yüklü hidrojen iyonlarınca engellenir; benzer şekilde, C elektrotuna göç eden fazla hidrojen iyonları da burada elektrokimyasal işlemle uzaklaştırılır. Sonuçta çözeltinin "yük"ü homojen kalır, fakat D elektrotunun çevresi, C elektrotunun çevresinden azalan miktar kadar sülfürik asitçe zenginleşir.
Çözeltideki elektrokimyasal reaksiyonlardan birinde hidrojen iyonları C den elektronları harcar; ikincisinde ise su molekülleri D de elektronlar oluşturur. Böylece, bu basit devrede üç çeşit elektrik geçişi bulunur; elektronik, iyonik, ve elektrokimyasal.
Ohm Kanunu: Bir devrede iki nokta arasındaki potansiyel V, direnç R olduğunda, I akımı (amper) aşağıdaki denklemle verilir, bu ifade ohm kanunu olarak bilinir. (Şekil-2a)
V= I R (4)
Ohm kanunu elektronik ve iyonik iletkenliğe uygulanabilir; ancak, Şekil-1’de görülen elektrot yüzeyleri gibi yüzeyler arasına uygulanamaz.
Akım Kanunu; Kirchhoff Birinci Kanunu: Bir devrede herhangi bir noktanın etrafındaki akımların cebirsel toplamı sıfırdır. (Şekil-2b)
Voltaj Kanunu; Kirchhoff İkinci Kanunu: Kapalı bir elektrik çevriminin (loop) etrafındaki voltajların cebirsel toplamı sıfırdır. Şekil-2c)
Şekil-2: Elektrik kanunları; (a) Ohm kanunu, (b) Kirchhoff birinci kanunu,
(c) Kirchhoff ikinci kanunu
Bir batarya, bir düğme, ve seri olarak bağlı üç direncin bulunduğu şekildeki basit devreyi inceleyelim. (Şekil-3a)
Şekil-3: (a) Basit bir seri devre ve, (b) bir voltaj bölücü devre
Devredeki D noktasına Kirchhoff akım kanunu uygulandığında,
I4 – I3 = 0 I4 = I3
yazılır. D nin dışındaki akımın giriş akımına göre zıt işaretli olduğuna dikkat edilmelidir. Benzer şekilde, C noktasına da ayni kanun uygulanır.
I3 = I2
Görüldüğü gibi, bir seri devrenin tüm noktalarında akım aynidir, veya,
I = I1 = I2 = I3 = I4
Devreye voltaj kanunu uygulanarak aşağıdaki eşitlikler yazılır.
V – V3 – V1 – V2 – V1 = 0
V = V1 + V2 + V3 (5)
D noktası C noktasına göre pozitiftir; ayni şekilde C noktası B noktasına göre, B noktası da A noktasına göre pozitiftir. Böylece, bataryanın V voltajını üç voltaj karşılar ve işaretleri V’nin işaretinin tersidir.
Denklem(5)’e Ohm kanunu uygulandığında aşağıdaki eşitlik elde edilir.
V = I (R1 + R2 + R3) = I R (6)
Bu seri devrenin toplam direnci her bir bileşenin dirençlerinin toplamına eşittir.
R = R1 + R2 + R3 (7)
Devrenin B noktasından A ya kadar olan kısmına Ohm kanunu uygulanarak,
V1 = I1 R1 = I R1
eşitliği yazılır. Bu eşitliğin Denklem(6) ya bölünmesiyle,
V1 I R1
¾¾ = ¾¾¾¾¾¾¾
V I (R1 +R2 +R3)
V R1 R1
V1 = ¾¾¾¾¾¾ = V ¾¾ (8)
R1 +R2 +R3 R
denklemi çıkarılır. Buna göre aşağıdaki eşitlikler de yazılabilir:
R2 R3
V2 = V ¾¾ V3 = V ¾¾
R R
Voltaj Bölücüler: Elektronik devrelerde, bir giriş voltajının değişken fonksiyonu olan potansiyellerin elde edilebilmesi için seri dirençler kullanılır. Bu tip cihazlara "voltaj bölücüler" denir. Şekil-3(a)’da görüldüğü gibi bunlardan bir tipi voltajları farklı aralıklarda böler; ikinci bir tip voltaj bölücü (Şekil-3b) sürekli değişen bir potansiyel verir, buna "potansiyometre" denir. Akım her yerde aynıdır:
Vi
I = ¾¾¾¾
R1 + R2
Çıkış voltajı aşağıdaki eşitlikle verilir; Vi = giriş voltajı, V0 = çıkış voltajıdır.
R1
V0 = ¾¾¾¾ Vi (9)
R1 + R2
4. Paralel Devreler
Şekil-4’de "paralel" bir DC devresi görülmektedir. A noktasına Kirchhoff akım kanunu uygulanarak aşağıdaki denklem çıkarılır.
Şekil-4: Paralel DC devresi
I1 + I2 + I3 – I = 0
I = I1 + I2 + I3 (10)
Kirchhoff voltaj kanunu üç bağımsız denklem verir:
V ve R1’in bulunduğu çevrim için: V = I1 R1
V ve R2’nin bulunduğu çevrim için: V = I2 R2
V ve R3’ün bulunduğu çevrim için: V = I3 R3
eşitlikleri yazılır. Ayrıca, R1 ile R2’nin ve R2 ile R3’ün bulunduğu çevrimler için de birer eşitlikler yazılabilir.
Bu son iki eşitlik önceki üç taneden bağımsız değildir. Eşitliklerin Denklem(10)’da yerine konulmasıyla Denklem(11) elde edilir.
V V V V
I = ¾¾ = ¾¾ = ¾¾ = ¾¾
R R1 R2 R3
1 1 1 1
¾¾ = ¾¾ + ¾¾ + ¾¾ (11)
R R1 R2 R3
R net devre direncidir. Paralel bir devrede, seri devrenin tersine, dirençler değil iletkenlikler (G) toplanabilir özelliktedir. G=1/R olduğundan Denklem(11),
G = G1 +G2 +G3 (12)
Şekilnde yazılır. Seri dirençlerin, voltaj bölücü olarak çalışmalarına karşın, paralel dirençler akım bölücü görevi yaparlar. Toplam akımın bir kısmı (R1’de bulunur) I1,
I1 V/R1 1/R1 G1
¾¾ = ¾¾¾ = ¾¾¾ = ¾¾
I V/R 1/R G
R G1
I1 = ¾¾ = ¾¾ (13)
R1 G
Şekildeki (1) devresinde; (a) toplam direnci,(b) bataryadan çekilen akımı, (c) her dirençteki potansiyel düşmesini, (d) her bir dirençteki akımları hesaplayınız.
(a). R2 ve R3 paralel dirençlerdir, bu nedenle A ve B noktaları arasındaki R2,3 direnci Denklem(11)’le verilir.
Şimdi, orijinal devreyi (2)’de görülen "eşdeğer devre" ye küçültebiliriz. Bu durumda, iki seri direncin bulunduğu bir devre elde edilmiştir; toplam direnç (R) bulunur:
R = R1 +R2,3 = 9.0 + 13.3 = 22.3 W
(b). Ohm kanunundan I akımı yazılır.
(c). Denklem(8) kullanılarak R1 boyunca olan V1 voltajı bulunur.
Benzer şekilde R2 ve R3 dirençlerindeki voltajlar hesaplanır.
İki voltajın toplamı (6.0 + 9.0) = 15 V’tur, bu da Kirchhoff kanuna uygundur.
(d). R1’deki akım, I1 = I = 0.67 A denklemiyle verilir. R2 ve R3’deki akımlar Ohm kanunu ile bulunur.
5. Alternatif Akım
Analitik sinyal transduserlerinden çıkan elektrik periyodik bir salınım gösterir. Bu salınımlar akım veya potansiyelin zamana göre grafiğe alınmasıyla gösterilebilir (Şekil-5). Sinyalin "periyodu, t" bir saykılın (devirin) tamamlanması için gerekli zamanı belirtir.
Periyot, t: Bir saykılın (devir) tamamlanması için gerekli zamanı belirtir.
t = 1/f s/devir
Frekans: Periyodun tersi saykılın "frekansı, f" dir. Frekans birimi hertz (Hz), 1 devir (saykıl)/saniye olarak tarif edilir.
f = 1 / t (14)
Genlik (amplitude), A: Denge halinden olan maksimum yer değiştirmedir.
i = Ip sin wt = Ip sin 2pft v = Vp sin wt = Vp sin 2pft
Ip ve Vp, pik akımı ve voltaj maksimumlarıdır.
Yayılma (propagation) hızı, v: w = açısal hız, rad/s, k’ = dalga sayısı, rad/m
w l
v = ¾¾ m/s v = ¾¾ m/s v = f l m/s
k’ t
Dalga boyu, l: Basit bir sinyalin bir periyotta aldığı mesafedir.
l = sinyal hızı x periyot m/devir
Vrms
Ohm Kanunu: AC devrede Ohm kanunu: Irms = ¾¾
Z
Z devrenin impedansı, V ve I voltaj ve akımın rms (veya etkin) değerleridir. Saf bir direnç için, Z = R dir. Vrms = Irms Z
Kapasitör için Ohm kanunu: Vrms = Irms XC
İndüktör için Ohm kanunu: Vrms = Irms XL
İmpedans: İmpedans, voltajın akıma oranı için kullanılan genel bir terimdir. Özel hallerde rezistans (direnç) veya reaktans olarak adlandırılır: f = 0 olduğunda, rezistans, = ± 900.olduğunda reaktans olarak tanımlanır.
Phasor Diyagramları
Sinüs dalgası, sabit bir hızla dönen bir vektörün izdüşümü (projeksiyon) olarak ifade edilebilir. Bu dönen vektöre phasor denir.
V = V0sin wt
ifadesi, V0 uzunluğundaki bir vektörün y-projeksiyonu olarak düşünülebilir; V0 vektörünün bir x-y düzleminde w açısal hızıyla döndüğü varsayılır.
İndüktör (VL), kapasitör (VC) ve direnç (VR) üzerindeki akım ve voltaj: Akım (I), daima VR’ye paraleldir. Voltaj vektörleri, akıma göre kendi faz konumlarını gösterir. f, akım ve voltaj arasındaki faz açısıdır.
Sinüs - Dalga Akımları: Sinüzoidal dalga (Şekil-5a) periyodik elektrik sinyal tipinin en çok karşılaşılanıdır. En iyi örnek, bir sarımın magnetik bir alan içinde döndürülmesiyle üretilen alternatif akımdır (bir elektrik jeneratörü gibi). Böylece, bir jeneratörün ürettiği akım veya voltajın zamana göre çizilen grafiği bir sinüs dalgası verir. Saf bir sinus dalgası sabit w açısal hızında, saat tersi yönde döner, Ip (veya Vp) uzunluğundaki vektör ile gösterilir (Şekil-7a). Vektör, t periyodu içinde 2p radyan hızla döner; açısal hız w, aşağıdaki ifade ile verilir.
2 p
w = ¾¾ = 2pf (15)
t
Vektör, akım veya voltaj ise, tam t zamanındaki akım (i) veya voltaj (v),
i = Ip sin w t = Ip sin 2 p f t (16)
v = Vp sin w t = Vp sin 2 p f t (17)
Ip ve Vp, pik akımı ve voltaj maksimumlarıdır; bunlara, sinus dalgasının "genliği (amplitude), A" denir. Şekil-7(b)'de genlikleri aynı iki sinus dalgası görülmektedir; iki dalga da 90 derece veya p/2 radyan "düzlem" dışıdır.
Şekil-7: (a) t periyotlu ve Ip genliğindeki bir sinüs dalgası, (b) genlikleri aynı iki sinüs dalgası
Faz farkına "faz açısı" denir, ve bir vektörün ikinci bir vektörden bu miktar kadar önce veya sonra olması durumunda ortaya çıkar. Bu tarife göre bir sinüs dalgası, genel anlamıyla, aşağıdaki eşitlikle verilir.
i = Ip sin (wt ± f) i = Ip sin (2pft ± f) (18)
f, referans bir sinüs dalgasına göre olan faz açısını gösterir. Benzer bir denklem de voltaj terimleriyle yazılabilir.
v = Vp sin (wt ± f) v = Vp sin (2pft ± f)
Bir sinüzoidal akımla ilgili akım veya voltaj çeşitli şekillerde tarif edilir. En basiti pik genliği Ip (veya Vp) dir, ve bir saykıl esnasındaki en yüksek (maksimum) akımdır (veya voltajdır); pik-pik değeri, 2Ip veya 2Vp de çok kullanılır. Bir ac devredeki "ortalama kare kök (root mean square)" veya "rms akımı", bir dirençte, ayni büyüklükteki bir doğru akımla ayni ısıtmayı yapar. Bu nedenle, rms akımı güç hesaplamalarında kullanılan (Denklem-2 ve 3) önemli bir değerdir. rms akımı aşağıdaki eşitlikle verilir.
rms Değerleri: Alternatif akımda ortalama akım veya voltaj (her ikisi de sıfır olduğundan) yerine ortalama kare kök, rms (root mean square) değerleri kullanılır.
rms akımı, bir dirençte, ayni büyüklükteki bir doğru akımla ayni ısıtmayı yapar. Bu nedenle, rms akımı güç hesaplamalarında kullanılan önemli bir değerdir.
AC Devrede Direnç: Direncin uçları arasındaki voltaj zamanla değiştiğinden, direnç boyunca olan akım da zamanla değişir. Voltaj ve akım faz içindedir; aynı anda pik (maks.) yaparlar.
V
iR = ¾¾ = Ip sin wt
R
Bir AC devredeki akım veya voltajın rms değerleri, basit bir doğru akım devredeki eşdeğer miktarlarla kıyaslanabilir.
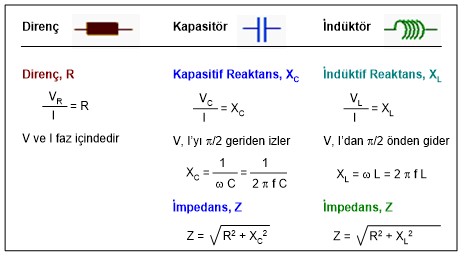
Kapasitif Reaktans: Devredeki kapasitörün akıma karşı gösterdiği dirençtir; XC ile tanımlanır. Reaktansın SI birimi Ohm, W = s/F
Kapasitör, I>0 olduğunda şarj, I<0 olduğunda deşarj konumundadır.
AC devrede kapasitör trafından harcanan ortalama güç sıfırdır. Her yarım devirde kapasitör enerjiyi toplar ve bir sonraki yerım devirde devreye boşaltır.
İndüktif Reaktans: Devredeki indüktörün akıma karşı gösterdiği dirençtir; XL ile tanımlanır (Şekil-8b).
XL = wL = 2pfL W
AC devrede indüktör için Ohm kanunu: Vrms = Irms XL
Reaktansın SI birimi Ohm, W = H/s Vrms = Irms XL
Voltaj akımdan 900 ilerde gider.
Akım çok hızlı değiştiğinde, voltaj maksimum olur. AC devrede indükör trafından harcanan ortalama güç sıfırdır.